
22.(本小题满分14分)
已知椭圆C的中心在原点,焦点在x轴上,经过点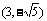 的直线l与向量(-2,
的直线l与向量(-2,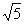 )平行且通过椭圆C的右焦点F,交椭圆C于A、B两点,又
)平行且通过椭圆C的右焦点F,交椭圆C于A、B两点,又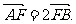
(1)求直线l的方程;
(2)求椭圆C的方程.
21.(本小题满分12分)
数列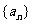 的前n项和Sn,当
的前n项和Sn,当 的等比中项
的等比中项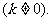
(1)求证:对于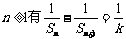 ;
;
(2)设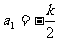 ,求Sn;
,求Sn;
(3)对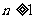 ,试证明:S1S2+S2S3+……+SnS
,试证明:S1S2+S2S3+……+SnS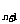
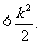
20.(本小题满分12分)
如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,CD=3AB.
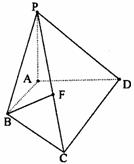 (1)点F在线段PC上运动,且设
(1)点F在线段PC上运动,且设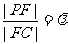 ,问当
,问当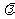 为何值时,BF//平面PAD?并证明你的结论;
为何值时,BF//平面PAD?并证明你的结论;
(2)在(1)成立的条件下,若BF⊥PC且AB=BF=1,
求四棱锥P-ABCD的体积.
19.(本小题满分12分)
已知: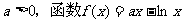
(1)设函数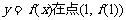 处的切线为
处的切线为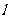 ,若
,若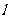 与圆
与圆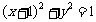 相切,求a的值;
相切,求a的值;
(2)求函数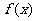 的单调区间.
的单调区间.
|
18.(本小题满分12分)
某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中三等奖的概率;
(2)求中奖的概率.
17.(本小题满分12分)
已知向量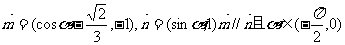
(1)求 的值;
的值;
(2)求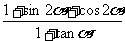 的值.
的值.
16.在技术工程中,场常用到双曲正弦函数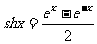 和双曲余弦函数
和双曲余弦函数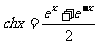 ,其实双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数相类似,比如关于正、余函数有
,其实双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数相类似,比如关于正、余函数有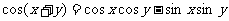 成立.而关于双曲正、余弦函数满足
成立.而关于双曲正、余弦函数满足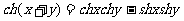 ,请你类比此关系式,写出关于双曲正弦、双曲余弦函数的一个新关系式
.
,请你类比此关系式,写出关于双曲正弦、双曲余弦函数的一个新关系式
.
14.把实数a,b,c,d排成形如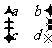 的形式,称之为二行二列矩陈。定义矩阵的一种运算
的形式,称之为二行二列矩陈。定义矩阵的一种运算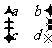 ·
·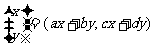 ,该运算的几何意义为平面上的点(x,y)在矩阵
,该运算的几何意义为平面上的点(x,y)在矩阵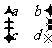 的作用下变换成点
的作用下变换成点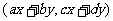 ,则点(2,3)在矩阵
,则点(2,3)在矩阵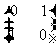 的作用下变换成点
.
的作用下变换成点
.
|
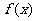 满足
满足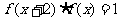 对于x∈R恒成立,且
对于x∈R恒成立,且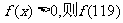 =
.
=
.13.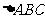 中,M是BC的中点,O是AM上一动点,若|AM|=6,则
中,M是BC的中点,O是AM上一动点,若|AM|=6,则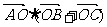 的最大值为
.
的最大值为
.
12.如图,三棱锥P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M、N分别在BC和PO上,且CM=x,PN=2CM,则下面四个图象中
大致描绘了三棱锥N-AMC的体积V与x变化关系(x∈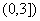

第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com