
7.将函数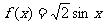 的图象按向量
的图象按向量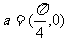 平移得到函数
平移得到函数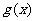 的图象,则
的图象,则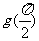 的值是 ( )
的值是 ( )
A.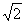 B.
B.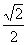 C.1 D.-
C.1 D.-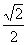
6.设直线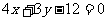 与两坐标轴分别交于A,B两点,若圆C的圆心在原点,且与线段AB有两个交点,则圆C的半径的取值范围是 ( )
与两坐标轴分别交于A,B两点,若圆C的圆心在原点,且与线段AB有两个交点,则圆C的半径的取值范围是 ( )
A.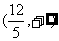 B.
B.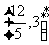 C.
C.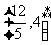 D.(3,4)
D.(3,4)
5.如果实数x、y满足条件 的最大值为 ( )
的最大值为 ( )
A.12 B.10 C.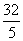 D.3
D.3
4.从4名男生和6名女生,选出3名升旗手,要求至少包含1名男生,则不同的选法共有
( )
A.160 B.100 C.200 D.140
3.若l,m表示直线,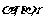 表示平面,则下列命题不正确的是 ( )
表示平面,则下列命题不正确的是 ( )
A.若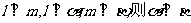 B.若
B.若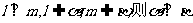
C.若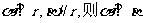 D.若
D.若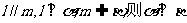
2.若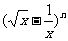 的展式开中第4项为常数项,则正整数n的值为 ( )
的展式开中第4项为常数项,则正整数n的值为 ( )
A.6 B.7 C.8 D.9
1.设集合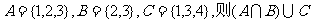 等于 ( )
等于 ( )
A.{1,2,3} B.{1,2,4} C.{1,3,4} D.{1,2,3,4}
22.(本小题满分14分)
已知函数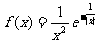
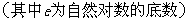
(Ⅰ)判断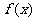 的奇偶性;
的奇偶性;
(Ⅱ)在 上求函数
上求函数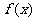 的极值;
的极值;
(Ⅲ)用数学归纳法证明:当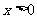 时,对任意正整数
时,对任意正整数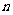 都有
都有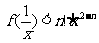
20.(本大题满分12分)在直角坐标平面上有一点列P1(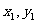 ),
),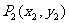 ,…,
,…,
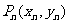 ,…对每个正整数
,…对每个正整数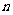 ,点
,点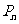 位于函数
位于函数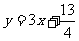 的图象上,且
的图象上,且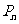 的横坐标构成以
的横坐标构成以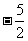 为首项,
为首项,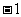 为公差的等差数列
为公差的等差数列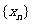 。
。
(1)求点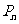 的坐标;
的坐标;
(2)设抛物线列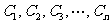 ,…中的每一条的对称轴都垂直于
,…中的每一条的对称轴都垂直于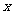 轴,第
轴,第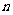 条抛物线
条抛物线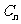 的顶点为
的顶点为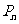 且过点
且过点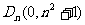 ,记过点
,记过点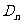 且与抛物线
且与抛物线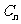 相切的直线的斜率为
相切的直线的斜率为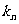 ,求证:
,求证: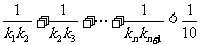 。
。
21 (本小题满分14分)
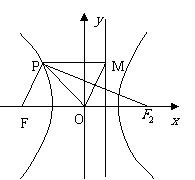 如图,若
如图,若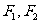 为双曲线
为双曲线
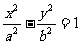 的左、右焦点,
的左、右焦点,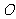 为坐标原点,
为坐标原点,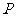 在双曲线左支
在双曲线左支
上,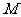 在右准线上,且满足
在右准线上,且满足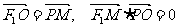
(Ⅰ)求此双曲线的离心率;
(Ⅱ)若此双曲线过点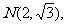 求双曲线的方程;
求双曲线的方程;
(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为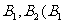 在y轴的正半轴上),过
在y轴的正半轴上),过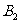 点作直线
点作直线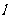 与双曲线交于
与双曲线交于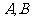 两点,当
两点,当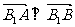 时,求直线
时,求直线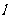 的方程。
的方程。
19. (本小题满分12分)
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=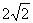 a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
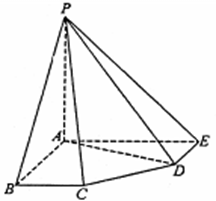 (Ⅰ)求证:PA⊥平面ABCDE;
(Ⅰ)求证:PA⊥平面ABCDE;
(Ⅱ)求二面角A-PD-E的大小;
(Ⅲ)求点C到平面PDE的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com