3．设(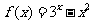，则在下列区间中，使函数f(x)有零点的区间是

　 A．[0,1]　　 　　 B．[1，2]　　 　　　 C.[-2，-1]　 　　　　　　 D．[-1，0]

2. 设实数a>1，复数z满足(1+ai)z＝i+a，则z对应的点在复平面中的

　 A．第一象限　 　　 B.第二象限　 　　　　　　 C．第三象限　 　　　 D.第四象限　

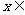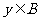1．已知集合A＝{2，3，4}，B＝{2，4，6，8}，C＝{(x，y)| A，，且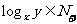}，则C中元素个数是

A．9　　 　　　　 B．8 　　　　　　　 C．3　　 　　　　　　 D．4

22．(本题满分13分)

　 　　　已知函数.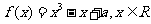

　 (1)求函数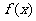在区间[-1，1]上的最大值与最小值；

　 (2)求证：对于区间[-1，1]上任意两个自变量的值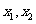，都有；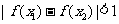

　 (3)若曲线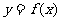上两点A、B 处的切线都与y 轴垂直，且线段AB与x轴有公共点，求a的取值范围。

21．(本题满分13分)

　　 　在直角坐标坐标系中，已知一个圆心在坐标原点，半径为2的圆，从这个圆上任意一点P向y轴作垂线段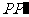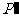，为垂足．

　　 (1)求线段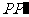中点M的轨迹C的方程；

　　 (2)过点Q(-2，0)作直线l与曲线C交于A、B两点，设N是过点(-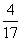，0)，且以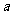=(0，1)为方向向量的直线上一动点，满足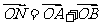(O为坐标原点)，问是否存在这样的直线l，使得四边形QANB为矩形?若存在，求出直线l的方程；若不存在，说明理由．

20．(本题满分12分)

　 　　设曲线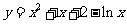在x=1处的切线为l，数列{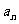}的首项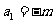，(其中常数m为正奇数)且对任意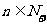，点(n-1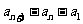，)均在直线l上。

　 (1)求出{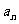}的通项公式；

　 (2)令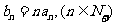，当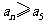恒成立时，求出n的取值范围，使得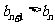成立．

19．(本题满分12分)

　　 某工厂有一段旧墙长14m，现准备利用这段旧墙为一面建造平面图形为矩形，面积为126m²的厂房，工程条件是：

　 (1)建1m新墙的费用为a元；(2)修1m旧墙的费用为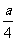元；(3)拆去1m的旧墙，用可得的建材建1m的新墙的费用为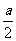元，经讨论有两种方案：

①利用旧墙一段xm(0<x<14)为矩形一边；

②矩形厂房利用旧墙的一面边长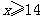，问如何利用旧墙建墙费最省？试比较①②两种方案哪个更好。

18．(本题满分12分)

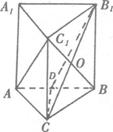
　 　　如图，在三棱柱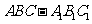中，侧棱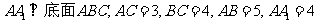,点D是AB的中点。

　 (1)求证：;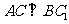

　 (2)求证：;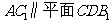

　 (3)求异面直线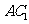与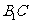所成角的余弦值。

17．(本题满分12分)

　 　　据市场调查，某种商品一年内每件出厂价在6千元的基础上，按月呈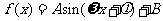的模型波动(x为月份)，已知3月份达到最高价8千元，7月份价格最低为4千元；该商品每件的售价为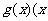为月份)，且满足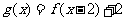

　 (1)分别写出该商品每件的出厂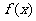价函数、售价函数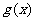的解析式；

　 (2)问哪几个月能盈利？

16．设集合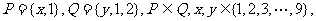且在直角坐标平面内，从所有满足这些条件的有序实数对(x，y)所表示的点中任取一个，其落在圆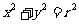内的概率恰为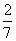，则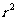的一个可能的整数值是　　　　　 (只需写出一个即可)

第Ⅱ卷