
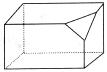
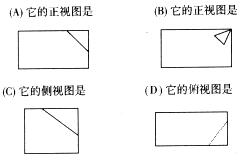
8.一个长方体去掉一角的直观图如右图所示,则下列图形画法正确的是
7.已知点A(3,3)、8(5,2)到直线ax+y+1=0的距离相等,则a的值是
(A)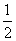 (B)-
(B)-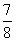 (c)
(c)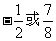 (D)
(D)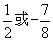
6.下列所给4个图象中,与所给3件事吻合最好的顺序为

(1)亮亮离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)亮亮骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)亮亮出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.

(A)(4)(1)(2) (B)(4)(2)(3) (C)(4)(1)(3) (D)(1)(2)(4)
5.函数y-ax在[0,1]上的最大值与最小值的和为4,则a= .
(A)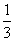 (B)3
(C)4 (D)
(B)3
(C)4 (D)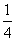
4.若P(2,1)为圆(x-1)2+y2-25的弦AB的中点,则直线AB的方程是
(A)x-y=0 (B)2x+y-3=0 (C)x+y-3=0 (D)2x-y-5=0
3.在下列四组函数中f(x)与g(x)表示同一函数的是
(A)f(x)=x-1,g(x)=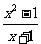
(B)
f(x)=|x+1|.g(x)=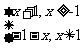
(C)f(x)=1,g(x)=(x+1)2
(D)f(x)=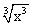 ,g(x)=(
,g(x)=(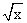 )2
)2
2.已知集合A={1,2},集合B满足A ∪B={1,2,3},则集合B有
(A)1个 (B)2个 (C)3个 (D)4个
1.若幂函数的图象过点(3,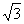
 ),则该函数的解析式是
),则该函数的解析式是
(A)y=x2 (B)y=x1/2 (C)y=x3 (D)y=x-1
(17)(本小题满分12分)
已知集合A=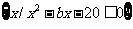 ,B=
,B=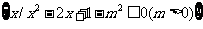 .
.
(I)求A,B;
(Ⅱ)若x∈A是x∈B的必要不充分条件,求实数m的范围.
(18)(本小题满分12分)
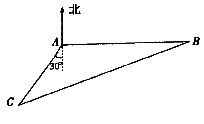
在信号站A处收到其正东方向,相距20浬的B处一艘渔船的求救信号,该信号站立即指挥在信号站A南偏西30°,与A相距10里的C处一快艇前往救援.
问:(I)B、C两处相距多少浬?
(Ⅱ)快艇应沿北偏东多少度的方向航行?
(arccos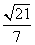 ≈49°)
≈49°)
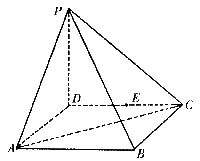
(19)(本小题满分12分)
四棱锥P-ABCD的底面ABCD为正方形,PD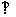 ABCD,且PD=AD.
ABCD,且PD=AD.
(I)求二面角C一PA-D的大小;
(II)若E为CD中点,在棱PB上是否存在一点F,使EF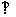 平面PAB,若存在,试确定点F的位置;若不存在,请说明理由.
平面PAB,若存在,试确定点F的位置;若不存在,请说明理由.
(20)(本小题满分12分)
某种汽车购买费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,以后每年递增0.2万元.
(Ⅰ)设使用n年该车的总费用(包括购车费用)为f(n),试写出f(n)的表达式;
(Ⅱ)求这种汽车使用多少年报废最合算(即汽车使用多少年年平均费用最少).
(21)(本小题满分12分)
公差不为零的等差数列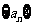 中,前三项和为15,且
中,前三项和为15,且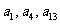 成等比数列.
成等比数列.
(I)求数列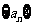 的通项公式
的通项公式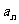 ;
;
(Ⅱ)设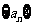 的前
的前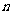 项和为
项和为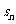 ,
,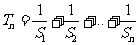 ,是否存在自然数
,是否存在自然数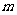 ,使
,使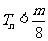 恒成立,若存在,求出
恒成立,若存在,求出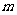 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(22)(本小题满分14分)
椭圆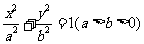 的焦点为Fl(-c,0),F2(c,0),中心为O,右顶点为A.椭圆上存在点P,满足
的焦点为Fl(-c,0),F2(c,0),中心为O,右顶点为A.椭圆上存在点P,满足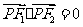 .
.
(I)求椭圆离心率的取值范围;
(Ⅱ)过F1的直线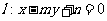 交椭圆于M、N两点,在椭圆离心率最小的情况下:
交椭圆于M、N两点,在椭圆离心率最小的情况下:
①当OM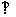 ON时,求m的值;
ON时,求m的值;
②当△AMN的面积最大值为 时,求椭圆的方程.
时,求椭圆的方程.
(13)各棱长均相等的正四陵锥,侧棱与底面所成的角为____
(14)在等比数列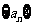 中,
中,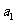 =2,
=2,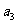 =1,则数列
=1,则数列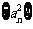 的前n项和为_________
的前n项和为_________
(15)某班去商店买钢笔和本子准备发奖,其中钢笔每支8元,本子每个6元,现有100元钱,要使买的件数最多,且用的钱数最多,则买到本子的个数为_____.
(16)下列关于圆锥曲线的命题:
①设A、B为两个定点,若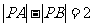 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②设A、B为两个定点,若动点P满足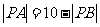 ,且
,且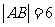 ,则
,则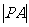 的最大值为8;
的最大值为8;
③方程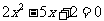 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线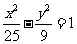 与椭圆
与椭圆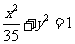 有相同的焦点.
有相同的焦点.
其中真命题的序号为________________(写出所有真命题的序号).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com