
1. 以下可以估计总体稳定性的统计量是 ( )
A. 样本平均数 B. 样本中位数 C. 样本方差 D. 样本最大值
(17)(本小题满分12分)
已知向量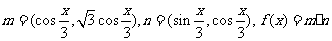 .
.
(I)求函数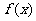 的单调区间;
的单调区间;
(Ⅱ)如果先将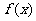 的图象向左平移
的图象向左平移 个单位,再保持纵坐标不变,横坐标变为原来的
个单位,再保持纵坐标不变,横坐标变为原来的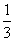
倍,得到函数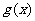 的图象.若
的图象.若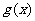 为偶函数,求
为偶函数,求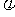 的最小值.
的最小值.
 (18)(本小题满分l2分)
(18)(本小题满分l2分)
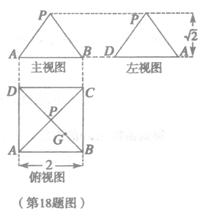
某几何体的三视图如图所示,P是正方形ABCD对角线的交
点,G是PB的中点.
(I)根据三视图,画出该几何体的直观图;
(Ⅱ)在直观图中,①证明: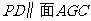 ;
;
②证明:面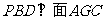 ;
;
③求面PAB与面PBC的夹角的余弦值.
(19)(本小题满分12分)
某厂生产一种产品,由于受生产能力和技术水平的限制,会产生一些次品.该厂生产这种产品的次品率p(p= )与日产量x(单位:件)之间满足关系
)与日产量x(单位:件)之间满足关系
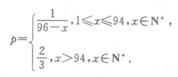
已知每生产一件合格品可盈利m元,但每生产一件次品将亏损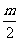 元.
元.
(I)判断日产量x超过94时,生产这种产品能否盈利?并说明理由;
(Ⅱ)当日产量x不超过94时,将该厂生产这种产品每天的盈利额y(元)表示成日产量x的函数;为了获得最高日盈利额,日产量应定为多少件?
(20)(本小题满分12分)
已知函数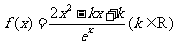
(I)k为何值时,函数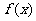 无极值;
无极值;
(Ⅱ)确定k的值,使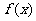 的极小值为0.
的极小值为0.
(21)(本小题满分12分)
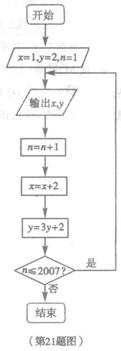
根据如图所示的程序框图,将输出的x、y值依次分别记为
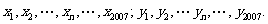
(I)求数列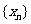 的通项公式
的通项公式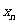 ;
;
(Ⅱ)写出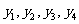 ,由此猜想出数列
,由此猜想出数列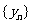 的一个通项公式
的一个通项公式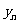 ,并证明你的结论;
,并证明你的结论;
(Ⅲ)求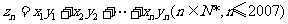
(22)(本小题满分l4分)
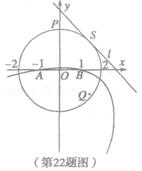
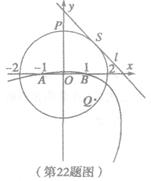
如图,已知圆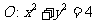 与y轴正半轴交于点P,
与y轴正半轴交于点P,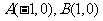 ,直线l与圆O切于点S (l 不垂直于x 轴),抛物线过A、B两点且以l为准线.
,直线l与圆O切于点S (l 不垂直于x 轴),抛物线过A、B两点且以l为准线.
(I)当点S在圆周上运动时,求证:抛物线的焦点Q 始终在某一椭圆C上,并求出该椭圆C的方程;
(Ⅱ)设M、N是(I)中椭圆C上除短轴端点外的不同两点,且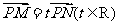 ,问:
,问: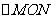 的面积是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
(13)已知实数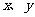 满足
满足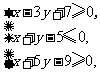 则
则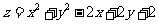 的最小值是
.
的最小值是
.
(14)曲线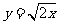 与直线
与直线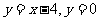 围成的图形的面积S =
.
围成的图形的面积S =
.
(15)聊城市某高级中学共有学生m名,编号为1,2,3,…,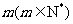 ;该校共开设了n门选修课,编号为1,2,3,…,
;该校共开设了n门选修课,编号为1,2,3,…,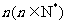 .定义记号
.定义记号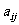 :若第i号学生选修了第j 号课程,则
:若第i号学生选修了第j 号课程,则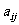 =1;否则
=1;否则
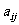 =0.如果
=0.如果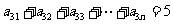 ,则该等式说明的实际含义是
,则该等式说明的实际含义是
(16)给出下列命题:
①样本方差反映了所有样本数据与样本平均值的偏离程度.
②若随机变量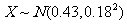 ,则此正态曲线在x=0.43处达到峰值.
,则此正态曲线在x=0.43处达到峰值.
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越差.
④市政府调查江北水城市民收入与市民旅游欲望的关系时,抽查了3000人.经过计算发现
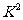 =6.023,则根据这一数据查阅下表,市政府有97.5%的把握认为市民收入与旅游欲望有关系.
=6.023,则根据这一数据查阅下表,市政府有97.5%的把握认为市民收入与旅游欲望有关系.
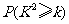 |
… |
0.25 |
0.15 |
0.10 |
0.025 |
0.010 |
0.O05 |
0.001 |
|
k |
… |
1.323 |
2.O72 |
2.706 |
5.024 |
6.635 |
7.879 |
10.888 |
其中正确命题的序号是 (注:把你认为正确的命题的序号都填上).
(1)设复数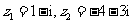 ,则
,则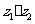 在复平面内对应的点位于
在复平面内对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(2)对函数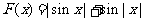 的性质的描述:①函数图象关于原点对称;②函数图象关于y轴对称;③该函数既有最大值又有最小值.
的性质的描述:①函数图象关于原点对称;②函数图象关于y轴对称;③该函数既有最大值又有最小值.
其中正确的个数为
(A)3 (B)2 (C)1 (D)O
(3)五一将至,小张制定了一项一日游计划,从江北水城的七个景点中选择5个进行游览.如果光岳楼、山陕会馆为必选景点,并且在游览过程中必须按先光岳楼后山陕会馆的次序经过两景点,则不同的游览线路有
(A)120种 (B)240种 (C)480种 (D)600种
(4)在正项等比数列{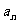 }中,
}中,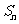 是其前n项和,若
是其前n项和,若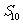 =10,
=10,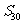 =130,则
=130,则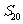 的值为
的值为
(A)50
(B)40
(C)30
(D)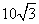
(5)“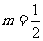 ”是“直线
”是“直线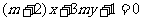 与直线
与直线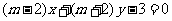 互相垂直”的
互相垂直”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
(6)已知函数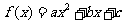 ,不等式
,不等式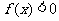 的解集为
的解集为 ,则函数
,则函数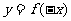
的图象可以为
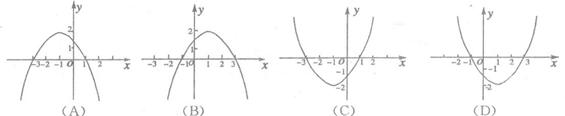
(7)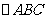 中,
中,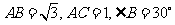 ,则
,则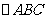 的面积等于
的面积等于
(A)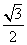 (B)
(B)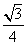 (C)
(C)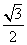 或
或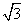 (D)
(D)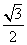 或
或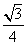
(8)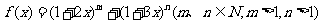 的展开式中x的系数是13,则
的展开式中x的系数是13,则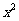 的系数为
的系数为
(A)31或40 (B)71或80 (C)31 (D)40
(9)设P、Q是两个非空集合,定义集合间的一种运算“⊙”: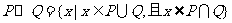 .
.
如果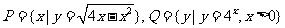 ,则
,则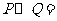
(A)[0,1]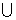 (4,+∞)
(B)[0,1]
(4,+∞)
(B)[0,1] 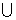 [4,+∞)
[4,+∞)
(C)[1,4] (D)(4,+∞)
(10)设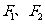 为双曲线
为双曲线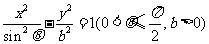 的两个焦点,过
的两个焦点,过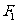 的直线交双曲线的同支于
的直线交双曲线的同支于
A、B两点,如果|AB|=m,则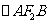 的周长的最大值是
的周长的最大值是
(A)4-m (B)4 (C)4+m (D)4+2m
(11)设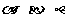 是三个不同的平面,
是三个不同的平面,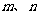 是两条不同的直线.在命题“
是两条不同的直线.在命题“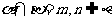 ,且
,则
,且
,则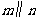 ”中的横线处填入下列三组条件中的一组,使该命题为真命题.
”中的横线处填入下列三组条件中的一组,使该命题为真命题.
①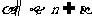 ;②
;②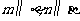 ;③
;③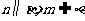 .
.
可以填入的条件有
(A)①或② (B)②或③ (C)①或③ (D)①或②或③
(12)设点A是半径为r、圆心为O的圆上一定点,点B是圆O内一点,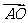 与
与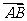 的夹角为
的夹角为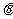 , 则
, 则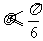 ,且
,且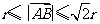 的概率为
的概率为
(A)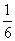 (B)
(B)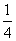 (C)
(C)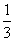 (D)
(D)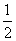
第Ⅱ卷 (非选择题 共90分)
(17)(本小题满分12分)
已知向量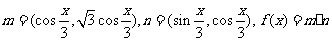 .
.
(I)求函数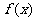 的单调区间;
的单调区间;
(Ⅱ)如果先将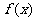 的图象向左平移
的图象向左平移 个单位,再保持纵坐标不变,横坐标变为原来的
个单位,再保持纵坐标不变,横坐标变为原来的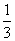
倍,得到函数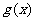 的图象.若
的图象.若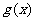 为偶函数,求
为偶函数,求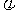 的最小值.
的最小值.
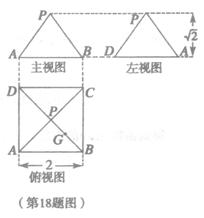 (18)(本小题满分l2分)
(18)(本小题满分l2分)
某几何体的三视图如图所示,P是正方形ABCD对角线的交
点,G是PB的中点.
(I)根据三视图,画出该几何体的直观图;
(Ⅱ)在直观图中,①证明: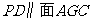 ;
;
②证明:面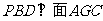 ;
;
(19)(本小题满分12分)
某厂生产一种产品,由于受生产能力和技术水平的限制,会产生一些次品.该厂生产这种产品的次品率p(p= )与日产量x(单位:件)之间满足关系
)与日产量x(单位:件)之间满足关系
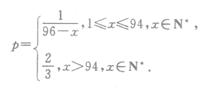
已知每生产一件合格品可盈利m元,但每生产一件次品将亏损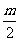 元.
元.
(I)判断日产量x超过94时,生产这种产品能否盈利?并说明理由;
(Ⅱ)当日产量x不超过94时,将该厂生产这种产品每天的盈利额y(元)表示成日产量x的函数;为了获得最高日盈利额,日产量应定为多少件?
(20)(本小题满分12分)
已知函数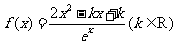
(I)k为何值时,函数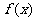 无极值;
无极值;
(Ⅱ)当k>4时,确定k的值,使 的极小值为0.
的极小值为0.
 (21)(本小题满分12分)
(21)(本小题满分12分)
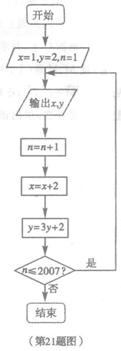
根据如图所示的程序框图,将输出的x、y值依次分别记为
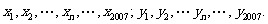
(I)求数列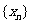 的通项公式
的通项公式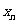 ;
;
(Ⅱ)写出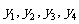 ,由此猜想出数列
,由此猜想出数列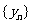 的一个通项公式
的一个通项公式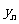 ,并证明你的结论;
,并证明你的结论;
(22)(本小题满分l4分)
如图,已知圆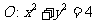 与y轴正半轴交于点P,
与y轴正半轴交于点P,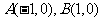 ,直线l与圆O切于点S (l
不垂直于x 轴),抛物线过A、B两点且以l为准线.
,直线l与圆O切于点S (l
不垂直于x 轴),抛物线过A、B两点且以l为准线.
(I)当点S在圆周上运动时,求证:抛物线的焦点Q 始终在某一椭圆C上,并求出该椭圆C的方程;
(Ⅱ)设M、N是(I)中椭圆C上除短轴端点外的不同两点,且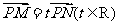 ,问:
,问: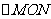 的面积是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
(13)已知实数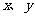 满足
满足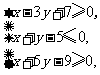 则
则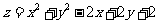 的最小值是
.
的最小值是
.
(14)已知曲线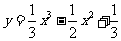 在
在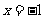 处的切线为l ,则过点P(-1,2)且与l垂直的直线方程为
.
处的切线为l ,则过点P(-1,2)且与l垂直的直线方程为
.
(15)聊城市某高级中学共有学生m名,编号为1,2,3,…,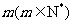 ;该校共开设了n门选修课,编号为1,2,3,…,
;该校共开设了n门选修课,编号为1,2,3,…,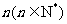 .定义记号
.定义记号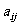 :若第i号学生选修了第j 号课程,则
:若第i号学生选修了第j 号课程,则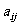 =1;否则
=1;否则
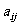 =0.如果
=0.如果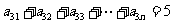 ,则该等式说明的实际含义是
,则该等式说明的实际含义是
(16)给出下列命题:
①样本方差反映了所有样本数据与样本平均值的偏离程度.
②若随机变量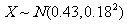 ,则此正态曲线在x=0.43处达到峰值.
,则此正态曲线在x=0.43处达到峰值.
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越差.
④市政府调查江北水城市民收入与市民旅游欲望的关系时,抽查了3000人.经过计算发现
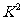 =6.023,则根据这一数据查阅下表,市政府有97.5%的把握认为市民收入与旅游欲望有关系.
=6.023,则根据这一数据查阅下表,市政府有97.5%的把握认为市民收入与旅游欲望有关系.
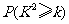 |
… |
0.25 |
0.15 |
0.10 |
0.025 |
0.010 |
0.O05 |
0.001 |
|
k |
… |
1.323 |
2.O72 |
2.706 |
5.024 |
6.635 |
7.879 |
10.888 |
其中正确命题的序号是 (注:把你认为正确的命题的序号都填上).
(1)设复数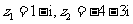 ,则
,则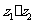 在复平面内对应的点位于
在复平面内对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(2)对函数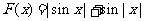 的性质的描述:①函数图象关于原点对称;②函数图象关于y轴对称;③该函数既有最大值又有最小值.其中正确的个数为
的性质的描述:①函数图象关于原点对称;②函数图象关于y轴对称;③该函数既有最大值又有最小值.其中正确的个数为
(A)3 (B)2 (C)1 (D)O
(3)某中学高一年级有学生x人,高二年级有学生900人,高三年级有学生y人。若采用分层抽样的方法抽一个容量为370人的样本,高一年级抽取120人,高三年级抽取100人,则该中学三个年级共有学生
(A)1900人 (B)2000人 (C)2100人 (D)2220人
(4)在正项等比数列{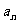 }中,
}中,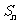 是其前n项和,若
是其前n项和,若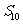 =10,
=10,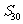 =130,则
=130,则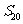 的值为
的值为
(A)50
(B)40 (C)30
(D)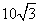
(5)“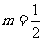 ”是“直线
”是“直线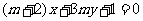 与直线
与直线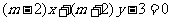 互相垂直”的
互相垂直”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
(6)已知函数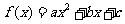 ,不等式
,不等式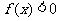 的解集为
的解集为 ,则函数
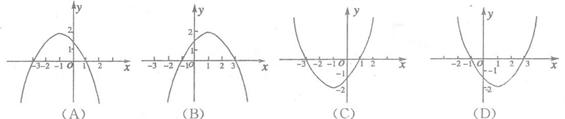
,则函数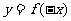
的图象可以为
(7)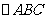 中,
中,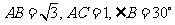 ,则
,则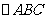 的面积等于
的面积等于
(A)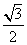 (B)
(B)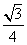 (C)
(C)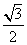 或
或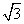 (D)
(D)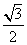 或
或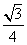
(8)设点A是圆O上一定点,点B是圆O上的动点,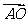 与
与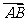 的夹角为
的夹角为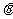 ,则
,则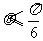 的概率为
的概率为
(A)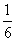 (B)
(B)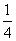 (C)
(C)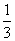 (D)
(D)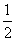
(9)设P、Q是两个非空集合,定义集合间的一种运算“⊙”: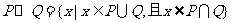 .
.
如果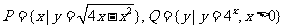 ,则
,则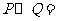
(A)[0,1]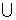 (4,+∞)
(B)[0,1]
(4,+∞)
(B)[0,1] 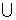 [4,+∞)
[4,+∞)
(C)[1,4] (D)(4,+∞)
(10)设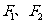 为双曲线
为双曲线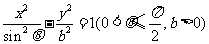 的两个焦点,过
的两个焦点,过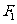 的直线交双曲线的同支于
的直线交双曲线的同支于
A、B两点,如果|AB|=m,则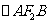 的周长的最大值是
的周长的最大值是
(A)4-m (B)4 (C)4+m (D)4+2m
(11)设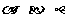 是三个不同的平面,
是三个不同的平面,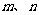 是两条不同的直线.在命题“
是两条不同的直线.在命题“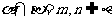 ,且 ,则
,且 ,则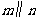 ”中的横线处填入下列三组条件中的一组,使该命题为真命题.
”中的横线处填入下列三组条件中的一组,使该命题为真命题.
①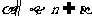 ;②
;②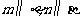 ;③
;③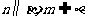 .
.
可以填入的条件有
(A)①或② (B)②或③ (C)①或③ (D)①或②或③
(12)设函数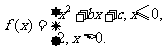 若
若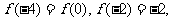 则函数
则函数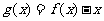 的零点的个数为
的零点的个数为
(A)3个 (B)2个 (C)1个 (D)0个
第Ⅱ卷 (非选择题 共90分)
20.(本小题满分13分)
如果函数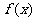 在区间D上有定义,且对任意
在区间D上有定义,且对任意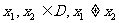 ,都有
,都有
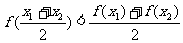 ,则称函数
,则称函数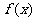 在区间D上的“凹函数”.
在区间D上的“凹函数”.
(Ⅰ)已知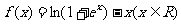 ,判断
,判断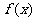 是否是“凹函数”,若是,请给出证明;若不是,请说明理由;
是否是“凹函数”,若是,请给出证明;若不是,请说明理由;
(Ⅱ)对于(I)中的函数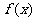 有下列性质:“若
有下列性质:“若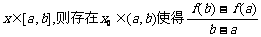
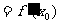 ”成立.利用这个性质证明
”成立.利用这个性质证明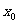 唯一;
唯一;
(Ⅲ)设A、B、C是函数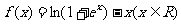 图象上三个不同的点,求证:
图象上三个不同的点,求证:
△ABC是钝角三角形.
19.(本小题满分13分)
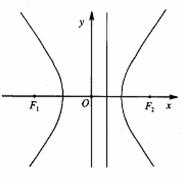
已知双曲线C的中心为坐标原点O,焦点F1、F2在x轴上,点P在双曲线的左支上,点
M在右准线上,且满足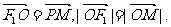
(Ⅰ)求双曲线C的离心率e;
(Ⅱ)若双曲线C过点Q(2,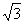 ),B1、B2是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且
),B1、B2是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且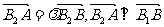 ,求直线AB的方程.
,求直线AB的方程.
18.(本小题满分13分)
已知函数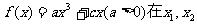 处分别取得极值
处分别取得极值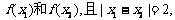
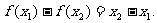
(Ⅰ)求函数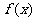 的解析式;
的解析式;
(Ⅱ)求函数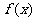 的单调区间与极值.
的单调区间与极值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com