
5.集合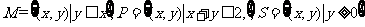 ,若
,若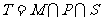 ,点
,点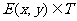 ,则
,则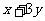 的最大值是
的最大值是
(A)O (B)2 (C)3 (D)4
4.函数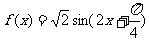 ,给出下列三个命题:
,给出下列三个命题:
①函数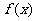 在区间[
在区间[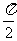 ,
,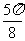 ]上是减函数;
]上是减函数;
②直线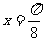 是函数
是函数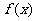 的图象的一条对称轴;
的图象的一条对称轴;
③函数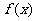 的图象可以由函数
的图象可以由函数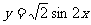 的图象向左平移
的图象向左平移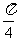 得到.其中正确的是
得到.其中正确的是
(A)①③ (B)①② (C)②③ (D)①②③
3.已知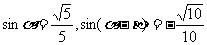 ,
,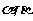 均为锐角,则
均为锐角,则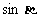 等于
等于
(A)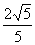 (B)
(B)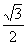 (C)
(C)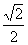 (D)
(D)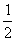
2.已知等差数列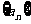 中,
中,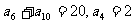 ,则
,则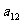 的值是
的值是
(A)26 (B)20 (C)18 (D)28
1. 在复平面内,复数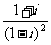 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
22.(本小题满分14分)
已知函数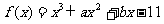 ,且
,且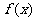 在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,又函数
在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,又函数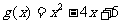 .
.
(Ⅰ)求函数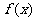 的解析式;
的解析式;
(Ⅱ)求证当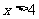 时,
时,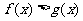 ;
;
(Ⅲ)若函数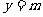 的图象与函数
的图象与函数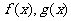 的图象共有3个交点,求
的图象共有3个交点,求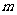 的取值范围。
的取值范围。
21.(本小题满分12分.)
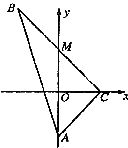
如图所示,△ABC为直角三角形,∠C=90°,若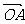 =(0,-4),M在
=(0,-4),M在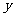 轴上,且AM=
轴上,且AM=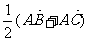 ,点C在
,点C在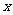 轴上移动.
轴上移动.
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,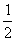 )的直线
)的直线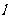 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,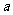 )(
)(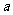 <0),
<0),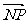 与
与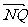 的夹角为
的夹角为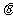 ,若
,若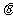 ≤
≤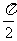 恒成立,求
恒成立,求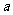 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以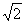 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求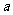 的值.
的值.
20.(本小题满分12分)
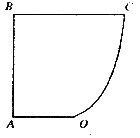
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=2AO=4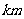 ,曲线段OC是以点0为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积.
,曲线段OC是以点0为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积.
19.(本小题满分12分J
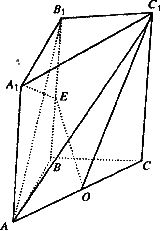
直三棱柱ABC-A1B1Cl中.已知AB=BC=AAl,∠ABC=90°,点O、E分别为AC、BBl的中点.
(Ⅰ)求证:OE//平面ABlC1;
(Ⅱ)求证:A1E⊥OC1.
18.(本小题满分12分)
已知各项均为正数的数列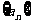 前
前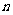 项和为
项和为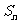 ,首项为
,首项为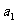 ,且2,
,且2,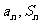 成等差数列.
成等差数列.
(Ⅰ)求数列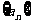 的通项公式
的通项公式
(Ⅱ)若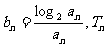 为数列
为数列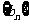 的前
的前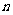 项和,
项和,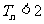 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com