
8.某商品进货规则是:不超过50件,按每件b元,若超过50件,按每件(b-30)元.现进货不超过50件花了a元,若在此基础上再多进11件,则花费仍为a元,设进货价都是每件整元,则a等于
A.1980 B.3690 C.6600 D.7200
7.若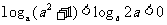 ,那么a的取值范围是
,那么a的取值范围是
A.(0,1) B. 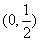 C.
C.
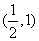 D.
D. 
6.从点(2,3)射出的光线沿与向量a=(8,4)平行的直线射到y轴上,则反射光线所在的直线方程
A. 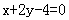 B.
B. 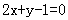 C.
C. 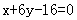 D.
D. 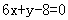
5.冥函数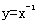 及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么冥函数
及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么冥函数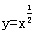 的图象经过的“卦限”是
的图象经过的“卦限”是
A. ④,⑦ B. ④,⑧ C. ③,⑧ D. ①,⑤
4.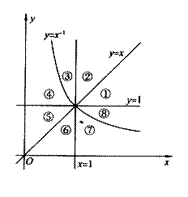 设集合I是全集,
设集合I是全集,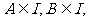 则“
则“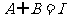 ”是“B=
”是“B=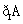 ”的
”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知直线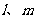 ,平面
,平面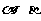 ,且
,且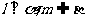 ,给出下列四个命题
,给出下列四个命题
①若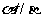 ,则
,则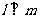 ②若
②若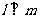 ,则
,则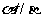
③若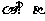 ,则
,则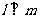 ④若
④若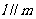 ,则
,则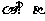
A. 1 B.2 C.3 D.4
2.已知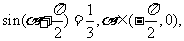 则
则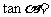
A. 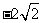 B.
B. 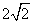 C.
C. 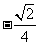 D.
D. 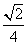
1. 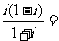
A.i B.-i C.1 D.-1
22.(本小题满分14分)
已知二次函数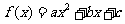 .
.
(1) 若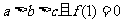 ,证明:f(x)的图象与x轴有两个相异交点;
,证明:f(x)的图象与x轴有两个相异交点;
(2) 证明:若对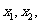 且
且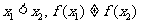 ,则方程
,则方程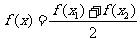 必有一实根在区间
必有一实根在区间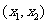 内;
内;
(3) 在(1)的条件下,设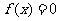 的另一个根为
的另一个根为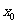 ,若方程
,若方程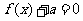 有解,证明
有解,证明 .
.
21.(本小题满分12分)
在自然条件下,一年中10次测量的某种细菌一天内存活时间的统计表(时间近似到0.1小时)如下表所示:
|
日期 |
1月 1日 |
2月 28日 |
3月 21日 |
4月 27日 |
5月 27日 |
6月 21日 |
8月 13日 |
9月 20日 |
10月 25日 |
12月 21日 |
|
日期位置序号x |
1 |
59 |
80 |
117 |
126 |
172 |
225 |
263 |
298 |
355 |
|
存活时间y(小时) |
5.6 |
10.2 |
12.3 |
16.4 |
17.3 |
19.4 |
16.4 |
12.5 |
8.5 |
5.4 |
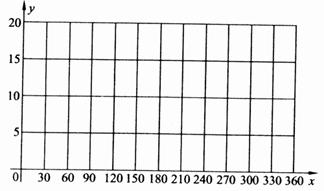
(1) 以日期在365天中的位置序号为横坐标,一天内存活时间为纵坐标,在给定坐标系中画出这些数据的散点图.
(2) 试选用一个形如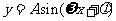 +t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
+t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
(3) 用(2)中的函数模型估计该种细菌一年中大约有多少天的存活时间大于15.9小时.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com