
4. 若平面向量a=(1,-2)与b的夹角是180°,且|b|=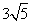 ,则b等于
,则b等于
A.(6,-3) B.(3,-6) C.(-3,6) D.(-6,3)
3. 对于平面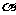 和共面的直线
和共面的直线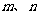 ,下列命题中是真命题的是
,下列命题中是真命题的是
A.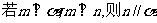 B.
B.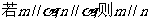
C.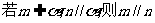 D.
D.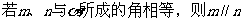
2.已知复数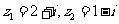 ,则
,则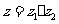 在复平面上对应的点位于
在复平面上对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
1.若集合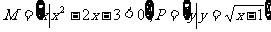 ,则M
,则M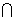 P等于
P等于
A.(0,3) B.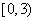 C.
C.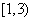 D.(-1,3)
D.(-1,3)
22.(本小题满分14分)
定义在 的三个函数f(x)、g(x)、h(x),已知f(x)=lnx, g(x)=
的三个函数f(x)、g(x)、h(x),已知f(x)=lnx, g(x)= 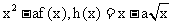 ,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
(I)求g(x),h(x)的表达式;
(II)求证:当1<x<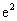 时,恒有
时,恒有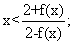
(III)把h(x)对应的曲线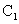 向上平移6个单位后得曲线
向上平移6个单位后得曲线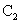 ,求
,求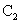 与g(x)对应曲线
与g(x)对应曲线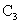 的交点个数,并说明道理.
的交点个数,并说明道理.
21.(本小题满分12分)
已知椭圆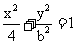 的焦点在x轴上,其右顶点关于直线x-y+4=0的对称点在直线
的焦点在x轴上,其右顶点关于直线x-y+4=0的对称点在直线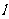 :
: 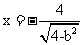 上.
上.
(I)求椭圆方程;
(II)过椭圆左焦点F的直线交椭圆于A、B两点,交直线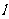 于点C,设O为坐标原点,且
于点C,设O为坐标原点,且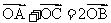 ,求
,求 ABC的面积.
ABC的面积.
20.(本小题满分12分)
 如图,在四棱锥P-ABCD中,PA
如图,在四棱锥P-ABCD中,PA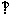 平面ABCD,底面ABCD是直线梯形,
平面ABCD,底面ABCD是直线梯形,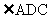 为直角,
为直角,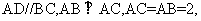 G是
G是 的重心,E为PB中点,F在线段BC上,且CF=2FB.
的重心,E为PB中点,F在线段BC上,且CF=2FB.
(I)证明:FG//平面PAB;
(II)证明:FG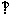 AC;
AC;
(III)求二面角P-CD-A的一个三角函数值,使得FG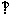 平面AEC
平面AEC
19.(本小题满分12分)
已知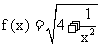 ,数列
,数列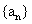 的前n项和为
的前n项和为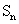 ,点
,点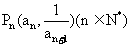 在曲线y=f(x)上,且
在曲线y=f(x)上,且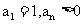 .
.
(I)求数列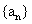 的通项公式
的通项公式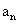 ;
;
(II)数列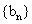 的首项
的首项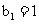 ,前n项和为
,前n项和为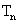 ,且
,且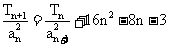 .求数列
.求数列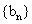 的通项公式
的通项公式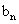 .
.
18.(本小题满分12分)
学校举行某项活动的选拔考试,规定参选者从备选的10道试题中抽取3道题进行测试,至少答对2道题才能入选.已知学生甲能答对备选题中的6道题,学生乙能答对备选题中的8道题.
(I)求学生甲对答对试题数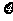 的分布及数学期望;
的分布及数学期望;
(II)求学生甲、乙至少有一人入选的概率.
17.(本小题满分12分)
设函数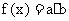 ,其中a=(2cosx,1),b=(cosx,
,其中a=(2cosx,1),b=(cosx,
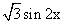 ),
),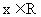 .
.
(I) 求f(x)的最大值;
(II)在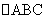 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且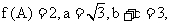 求b、c的值.
求b、c的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com