
2. 如果复数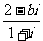 的实部和虚部互为相反数,则b的值等于
的实部和虚部互为相反数,则b的值等于
(A)0 (B)1 (C)2 (D)3
1.设全集U=R,A={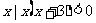 },B={
},B={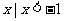 },则图中阴影部分表示的集合为
},则图中阴影部分表示的集合为
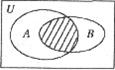
(A){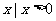 }
(B){
}
(B){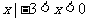 }
}
(C){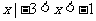 } (D){
} (D){ 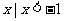 }
}
(18)(本题14分)已知△ABC的周长为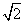 +1,且sinA+sin B=
+1,且sinA+sin B=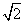 sin C
sin C
(I)求边AB的长;
(Ⅱ)若△ABC的面积为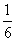 sin C,求角C的度数.
sin C,求角C的度数.
(19)(本题14分)已知数列{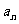 }中的相邻两项
}中的相邻两项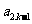 、
、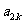 是关于x的方程
是关于x的方程
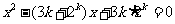 的两个根,且
的两个根,且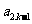 ≤
≤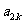 (k =1,2,3,…).
(k =1,2,3,…).
(I)求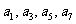 及
及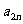 (n≥4)(不必证明);
(n≥4)(不必证明);
(Ⅱ)求数列{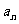 }的前2n项和S2n.
}的前2n项和S2n.
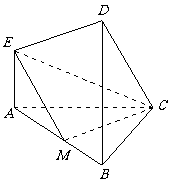 (20)(本题14分)在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点.
(20)(本题14分)在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点.
(I)求证:CM ⊥EM:
(Ⅱ)求DE与平面EMC所成角的正切值.
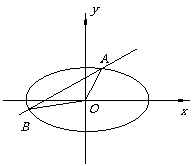 (21)(本题15分)如图,直线y=kx+b与椭圆
(21)(本题15分)如图,直线y=kx+b与椭圆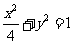 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
(I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
(22)(本题15分)已知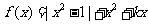 .
.
(I)若k=2,求方程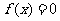 的解;
的解;
(II)若关于x的方程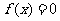 在(0,2)上有两个解x1,x2,求k的取值范围,并证明
在(0,2)上有两个解x1,x2,求k的取值范围,并证明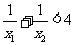
(11)函数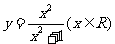 的值域是______________.
的值域是______________.
(12)若sinθ+cosθ=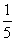 ,则sin 2θ的值是________.
,则sin 2θ的值是________.
(13)某校有学生2000人,其中高三学生500人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高三学生的人数为___________.
(14)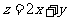 中的
中的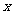 、
、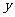 满足约束条件
满足约束条件 则
则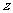 的最小值是_________.
的最小值是_________.
(15)曲线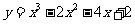 在点(1,一3)处的切线方程是___________ .
在点(1,一3)处的切线方程是___________ .
(16)某书店有11种杂志,2元1本的8种,1元1本的3种.小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是__________(用数字作答).
(17)已知点O在二面角α-AB-β的棱上,点P在α内,且∠POB=45°.若对于β内异于O的任意一点Q,都有∠POQ≥45°,则二面角α-AB-β的大小是_________.
(1)设全集U={1,3,5,6,8},A={1,6},B={5,6,8},则(CUA)∩B=
(A){6} (B){5,8} (C){6,8} (D){3,5,6,8}
(2)已知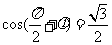 ,且
,且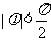 ,则tan
,则tan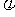 =
=
(A)-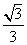 (B)
(B) 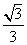 (C) -
(C) -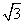 (D)
(D) 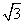
(3)“x>1”是“x2>x”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(4)直线x-2y+1=0关于直线x=1对称的直线方程是
(A)x+2y-1=0 (B)2 x+y-1=0
(C)2 x+y-3=0 (D) x+2y-3=0
 (5)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是
(5)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是
(A) 6 (B) 5 (C) 4 (D) 3
(6)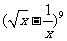 展开式中的常数项是
展开式中的常数项是
(A) -36 (B)36 (C) -84 (D) 84
(7)若P是两条异面直线l、m外的任意一点,则
(A)过点P有且仅有一条直线与l、m都平行
(B)过点P有且仅有一条直线与l、m都垂直
(C)过点P有且仅有一条直线与l、m都相交
(D)过点P有且仅有一条直线与l、m都异面
(8)甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是
(A) 0.216 (B)0.36 (C)0.432 (D)0.648
(9)若非零向量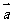 、
、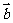 满足|
满足|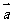 一
一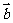 |=|
|=|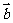 |,则
|,则
(A) |2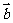 |>|
|>|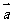 一2
一2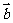 | (B) |2
| (B) |2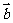 |<|
|<|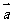 一2
一2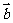 |
|
(C) |2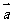 |>|2
|>|2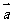 一
一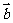 | (D) |2
| (D) |2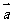 |<|2
|<|2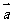 一
一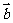 |
|
(10)已知双曲线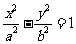
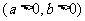 的左、右焦点分别为F1、F2,P是准线上一点,且P F1⊥P F2,|P F1|
的左、右焦点分别为F1、F2,P是准线上一点,且P F1⊥P F2,|P F1|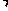 |P F2 |=4ab,则双曲线的离心率是
|P F2 |=4ab,则双曲线的离心率是
(A)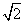 (B)
(B) 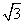 (C)2 (D)3
(C)2 (D)3
(18)(本题14分)已知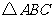 的周长为
的周长为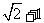 ,且
,且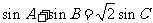 .
.
(I)求边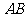 的长;
的长;
(II)若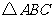 的面积为
的面积为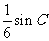 ,求角
,求角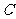 的度数.
的度数.
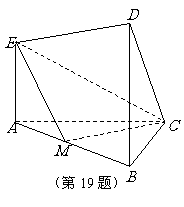
(19)(本题14分)在如图所示的几何体中,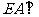 平面
平面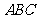 ,
,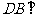 平面
平面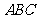 ,
,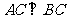 ,且
,且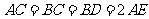 ,
,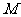 是
是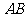 的中点.
的中点.
(I)求证: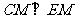 ;
;
(II)求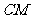 与平面
与平面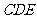 所成的角.
所成的角.
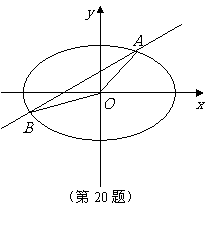
 (20)(本题14分)如图,直线
(20)(本题14分)如图,直线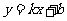 与椭圆
与椭圆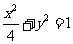 交于
交于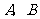 两点,记
两点,记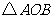 的面积为
的面积为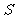 .
.
(I)求在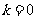 ,
,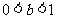 的条件下,
的条件下,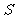 的最大值;
的最大值;
(II)当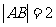 ,
,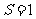 时,求直线
时,求直线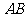 的方程.
的方程.
(21)(本题15分)已知数列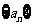 中的相邻两项
中的相邻两项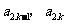 是关于
是关于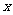 的方程
的方程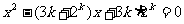 的两个根,且
的两个根,且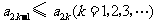 .
.
(I)求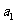 ,
,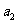 ,
,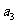 ,
,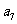 ;
;
(II)求数列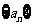 的前
的前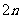 项和
项和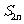 ;
;
(Ⅲ)记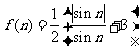 ,
,
 ,
,
求证: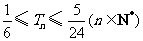 .
.
(22)(本题15分)设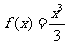 ,对任意实数
,对任意实数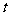 ,记
,记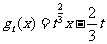 .
.
(I)求函数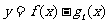 的单调区间;
的单调区间;
(II)求证:
(ⅰ)当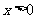 时,
时,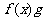
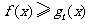 对任意正实数
对任意正实数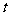 成立;
成立;
(ⅱ)有且仅有一个正实数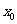 ,使得
,使得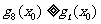 对任意正实数
对任意正实数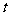 成立.
成立.
(11)已知复数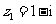 ,
,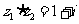 ,则复数
,则复数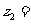 .
.
(12)已知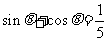 ,且
,且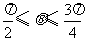 ,则
,则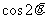 的值是
.
的值是
.
(13)不等式 的解集是 .
的解集是 .
(14)某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答).
(15)随机变量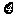 的分布列如下:
的分布列如下:
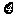
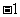
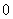
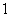
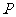
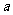
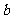
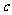
其中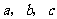 成等差数列,若
成等差数列,若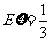 ,则
,则 的值是
.
的值是
.
(16)已知点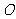 在二面角
在二面角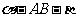 的棱上,点
的棱上,点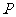 在
在 内,且
内,且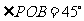 .若对于
.若对于 内异于
内异于 的任意一点
的任意一点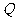 ,都有
,都有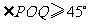 ,则二面角
,则二面角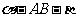 的大小是 .
的大小是 .
(17)设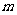 为实数,若
为实数,若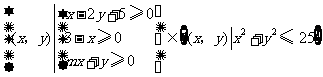 ,则
,则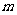 的取值范围是
.
的取值范围是
.
(1)“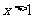 ”是“
”是“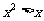 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分不必要条件 D.既不充分也不必要条件
(2)若函数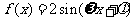 ,
,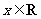 (其中
(其中 ,
,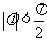 )的最小正周期是
)的最小正周期是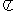 ,且
,且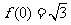 ,则( )
,则( )
A.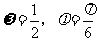 B.
B.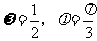
C.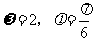 D.
D.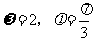
(3)直线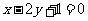 关于直线
关于直线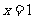 对称的直线方程是( )
对称的直线方程是( )
A.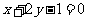 B.
B.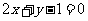
 C.
C.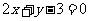 D.
D.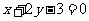
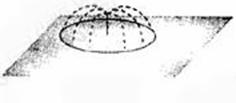
(4)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是( )
A.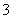 B.
B.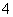 C.
C.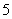 D.
D.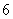
(5)已知随机变量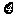 服从正态分布
服从正态分布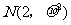 ,
,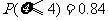 ,则
,则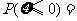 ( )
( )
A.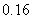 B.
B.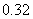 C.
C.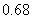 D,
D,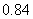
(6)若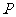 两条异面直线
两条异面直线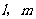 外的任意一点,则( )
外的任意一点,则( )
A.过点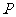 有且仅有一条直线与
有且仅有一条直线与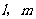 都平行
都平行
B.过点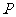 有且仅有一条直线与
有且仅有一条直线与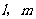 都垂直
都垂直
C.过点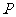 有且仅有一条直线与
有且仅有一条直线与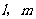 都相交
都相交
D.过点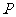 有且仅有一条直线与
有且仅有一条直线与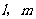 都异面
都异面
(7)若非零向量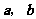 满足
满足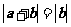 ,则( )
,则( )
A.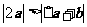 B.
B.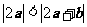
C.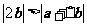 D.
D. 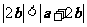
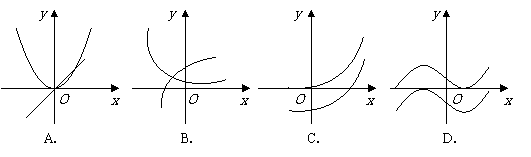
(8)设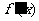 是函数
是函数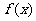 的导函数,将
的导函数,将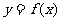 和
和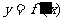 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )
(9)已知双曲线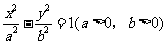 的左、右焦点分别为
的左、右焦点分别为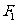 ,
,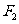 ,
,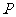 是准线上一点,且
是准线上一点,且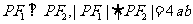 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.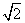 B.
B.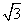 C.
C.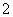 D.
D.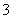
(10)设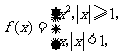
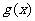 是二次函数,若
是二次函数,若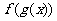 的值域是
的值域是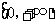 ,则
,则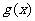 的值域是( )
的值域是( )
A.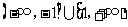 B.
B.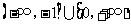
C.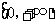 D.
D.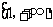
第II卷(共100分)
(17)(本小题满分12分)
已知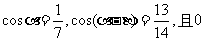 <
<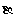 <
<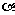 <
<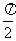 ,
,
(Ⅰ)求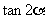 的值.
的值.
(Ⅱ)求 .
.
(18)(本小题满分12分)
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数 的分布列及期望
的分布列及期望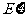 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
(19)(本小题满分12分)
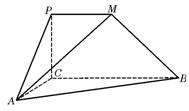 如图,
如图,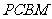 是直角梯形,∠
是直角梯形,∠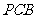 =90°,
=90°,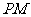 ∥
∥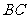 ,
,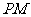 =1,
=1,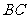 =2,又
=2,又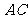 =1,∠
=1,∠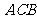 =120°,
=120°,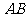 ⊥
⊥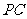 ,直线
,直线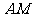 与直线
与直线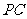 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面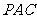 ⊥平面
⊥平面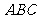 ;
;
(Ⅱ)求二面角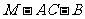 的大小;
的大小;
(Ⅲ)求三棱锥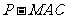 的体积.
的体积.
(20)(本小题满分12分)
设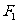 、
、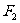 分别是椭圆
分别是椭圆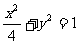 的左、右焦点.
的左、右焦点.
(Ⅰ)若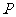 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求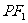 ·
·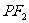 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点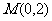 的直线
的直线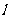 与椭圆交于不同的两点
与椭圆交于不同的两点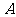 、
、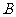 ,且∠
,且∠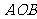 为锐角(其中
为锐角(其中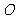 为坐标原点),求直线
为坐标原点),求直线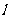 的斜率
的斜率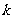 的取值范围.
的取值范围.
(21).(本小题满分12分)
已知函数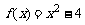 ,设曲线
,设曲线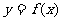 在点(
在点(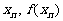 )处的切线与
)处的切线与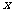 轴线发点(
轴线发点(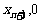 )(
)(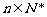 )其中
)其中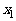 为正实数
为正实数
(Ⅰ)用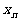 表示
表示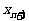
(Ⅱ)求证:对于一切正整数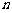 ,
,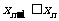 的充要条件是
的充要条件是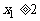 ;
;
(Ⅲ)若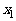 =4,记
=4,记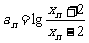 ,证明数列
,证明数列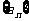 成等比数列,并求数列
成等比数列,并求数列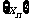 的通项公式
的通项公式
(22)(本小题满分14分)
设函数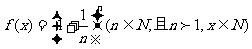 .
.
(Ⅰ)当x=6时,求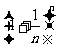 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明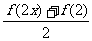 >
>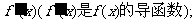
(Ⅲ)是否存在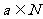 ,使得an<
,使得an<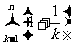 <
<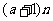 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
(13)若函数f(x)=e-(m-u)2 (c是自然对数的底数)的最大值是m,且f(x)是偶函数,则m+u= .
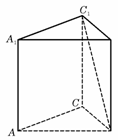
(14)如图,在正三棱柱ABC-A1B1C1中,侧棱长为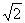 ,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是 .
,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是 .
(15)已知⊙O的方程是x2+y2-2=0, ⊙O’的方程是x2+y2-8x+10=0,由动点P向⊙O和⊙O’所引的切线长相等,则动点P的轨迹方程是 .
(16)下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是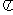 .
.
②终边在y轴上的角的集合是{a|a=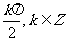 |.
|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数
⑤函数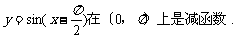
其中真命题的序号是 (写出所言 )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com