
3.设A={x|1<x<2},B={x|x>a},若A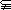 B,则a的取值范围是___________________.
B,则a的取值范围是___________________.
解析:A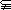 B说明A是B的真子集,利用数轴(如下图)可知a≤1.
B说明A是B的真子集,利用数轴(如下图)可知a≤1.
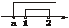
答案:a≤1
2.(2004年上海,3)设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B=______________.
解析:∵A∩B={2},∴log2(a+3)=2.
∴a=1.∴b=2.
∴A={5,2},B={1,2}.∴A∪B={1,2,5}.
答案:{1,2,5}
1.集合A={(x,y)|x+y=0},B={(x,y)|x-y=2},则A∩B是
A.(1,-1) B.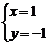
C.{(1,-1)} D.{1,-1}
解析: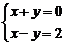
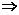
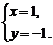
答案:C
5.已知集合A={0,1},B={x|x∈A,x∈N*},C={x|x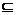 A},则A、B、C之间的关系是___________________.
A},则A、B、C之间的关系是___________________.
解析:用列举法表示出B={1},C={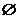 ,{1},{0},A},易见其关系.这里A、B、C是不同层次的集合,C以A的子集为元素,同一层次的集合可有包含关系,不同层次的集合之间只能是从属关系.
,{1},{0},A},易见其关系.这里A、B、C是不同层次的集合,C以A的子集为元素,同一层次的集合可有包含关系,不同层次的集合之间只能是从属关系.
答案:B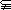 A,A∈C,B∈C
A,A∈C,B∈C
●典例剖析
[例1] (2004年北京,8)函数f(x)=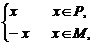 其中P、M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断,其中正确判断有
其中P、M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断,其中正确判断有
①若P∩M=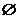 ,则f(P)∩f(M)=
,则f(P)∩f(M)=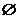 ②若P∩M≠
②若P∩M≠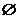 ,则f(P)∩f(M)≠
,则f(P)∩f(M)≠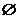 ③若P∪M=R,则f(P)∪f(M)=R ④若P∪M≠R,则f(P)∪f(M)≠R
③若P∪M=R,则f(P)∪f(M)=R ④若P∪M≠R,则f(P)∪f(M)≠R
A.1个 B.2个 C.3个 D.4个
剖析:由题意知函数f(P)、f(M)的图象如下图所示.
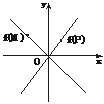
设P=[x2,+∞),M=(-∞,x1],∵|x2|<|x1|,f(P)=[f(x2),+∞),f(M)=[f(x1),+∞),则P∩M=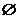 .
.
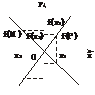
而f(P)∩f(M)=[f(x1),+∞)≠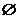 ,故①错误.同理可知②正确.设P=[x1,+∞),M=(-∞,x2],∵|x2|<|x1|,则P∪M=R.
,故①错误.同理可知②正确.设P=[x1,+∞),M=(-∞,x2],∵|x2|<|x1|,则P∪M=R.
f(P)=[f(x1),+∞),f(M)=[f(x2),+∞),
f(P)∪f(M)=[f(x1),+∞)≠R,故③错误.同理可知④正确.
答案:B
[例2] 已知A={x|x3+3x2+2x>0},B={x|x2+ax+b≤0}且A∩B={x|0<x≤2},A∪B={x|x>-2},求a、b的值.
解:A={x|-2<x<-1或x>0},
设B=[x1,x2],由A∩B=(0,2]知x2=2,
且-1≤x1≤0, ①
由A∪B=(-2,+∞)知-2≤x1≤-1. ②
由①②知x1=-1,x2=2,
∴a=-(x1+x2)=-1,b=x1x2=-2.
评述:本题应熟悉集合的交与并的涵义,熟练掌握在数轴上表示区间(集合)的交与并的方法.
深化拓展
(2004年上海,19)记函数f(x)=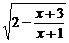 的定义域为A,g(x)=
的定义域为A,g(x)=
lg[(x-a-1)(2a-x)](a<1)的定义域为B.
(1)求A;
(2)若B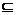 A,求实数a的取值范围.
A,求实数a的取值范围.
提示:(1)由2-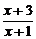 ≥0,得
≥0,得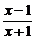 ≥0,
≥0,
∴x<-1或x≥1,即A=(-∞,-1)∪[1,+∞).
(2)由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a.∴B=(2a,a+1).
∵B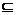 A,∴2a≥1或a+1≤-1,即a≥
A,∴2a≥1或a+1≤-1,即a≥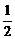 或a≤-2.
或a≤-2.
而a<1,∴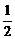 ≤a<1或a≤-2.
≤a<1或a≤-2.
故当B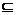 A时,实数a的取值范围是(-∞,-2]∪[
A时,实数a的取值范围是(-∞,-2]∪[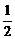 ,1).
,1).
[例3] (2004年湖北,10)设集合P={m|-1<m≤0},Q={m∈R|mx2+4mx-4<0对任意实数x恒成立},则下列关系中成立的是
A.P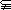 Q B.Q
Q B.Q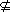 P C.P=Q D.P∩Q=Q
P C.P=Q D.P∩Q=Q
剖析:Q={m∈R|mx2+4mx-4<0对任意实数x恒成立},
对m分类:①m=0时,-4<0恒成立;
②m<0时,需Δ=(4m)2-4×m×(-4)<0,解得m<0.
综合①②知m≤0,∴Q={m∈R|m≤0}.
答案:A
评述:本题容易忽略对m=0的讨论,应引起大家足够的重视.
[例4] 已知集合A={(x,y)|x2+mx-y+2=0},B={(x,y)|x-y+1=0,0≤x≤2},如果A∩B≠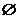 ,求实数m的取值范围.
,求实数m的取值范围.
剖析:如果目光总是停留在集合这一狭窄的知识范围内,此题的思维方法是很难找到的.事实上,集合符号在本题中只起了一种“化妆品”的作用,它的实际背景是“抛物线x2+mx-y+2=0与线段x-y+1=0(0≤x≤2)有公共点,求实数m的取值范围”.这种数学符号与数学语言的互译,是考生必须具备的一种数学素质.
解:由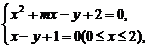 得
得
x2+(m-1)x+1=0. ①
∵A∩B≠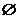 ,∴方程①在区间[0,2]上至少有一个实数解.
,∴方程①在区间[0,2]上至少有一个实数解.
首先,由Δ=(m-1)2-4≥0,得m≥3或m≤-1.
当m≥3时,由x1+x2=-(m-1)<0及x1x2=1知,方程①只有负根,不符合要求;
当m≤-1时,由x1+x2=-(m-1)>0及x1x2=1>0知,方程①有两个互为倒数的正根.故必有一根在区间(0,1]内,从而方程①至少有一个根在区间[0,2]内.
综上所述,所求m的取值范围是(-∞,-1].
评述:上述解法应用了数形结合的思想.如果注意到抛物线x2+mx-y+2=0与线段x-y+1=0(0≤x≤2)的公共点在线段上,本题也可以利用公共点内分线段的比λ的取值范围建立关于m的不等式来解.
深化拓展
设m∈R,A={(x,y)|y=-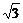 x+m},B={(x,y)|x=cosθ,y=sinθ,0<θ<2π},且A∩B={(cosθ1,sinθ1),(cosθ2,sinθ2)}(θ1≠θ2),求m的取值范围.
x+m},B={(x,y)|x=cosθ,y=sinθ,0<θ<2π},且A∩B={(cosθ1,sinθ1),(cosθ2,sinθ2)}(θ1≠θ2),求m的取值范围.
提示:根据题意,直线y=-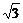 x+m与圆x2+y2=1(x≠1)交于两点,
x+m与圆x2+y2=1(x≠1)交于两点,
∴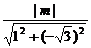 <1且0≠-
<1且0≠-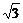 ×1+m.
×1+m.
∴-2<m<2且m≠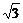 .
.
答案:-2<m<2且m≠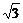 .
.
●闯关训练
夯实基础
4.设U是全集,非空集合P、Q满足P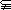 Q
Q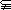 U,若求含P、Q的一个集合运算表达式,使运算结果为空集
U,若求含P、Q的一个集合运算表达式,使运算结果为空集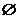 ,则这个运算表达式可以是_______________.
,则这个运算表达式可以是_______________.
解析:构造满足条件的集合,实例论证.
U={1,2,3},P={1},Q={1,2},则(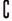 UQ)={3},(
UQ)={3},(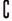 UP)={2,3},易见(
UP)={2,3},易见(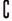 UQ)∩P=
UQ)∩P=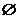 .
.
答案:(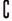 UQ)∩P
UQ)∩P
3.(2004年天津,1)设集合P={1,2,3,4,5,6},Q={x∈R|2≤x≤6},那么下列结论正确的是
A.P∩Q=P
B.P∩Q Q
Q
C.P∪Q=Q
D.P∩Q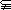 P
P
解析:P∩Q={2,3,4,5,6},∴P∩Q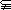 P.
P.
答案:D
2.(2005年北京西城区抽样测试题)已知集合A={x∈R|x<5-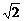 },B={1,2,3,4},则(
},B={1,2,3,4},则(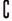 RA)∩B等于
RA)∩B等于
A.{1,2,3,4} B.{2,3,4}
C.{3,4} D.{4}
解析: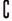 RA={x∈R|x≥5-
RA={x∈R|x≥5-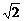 },而5-
},而5-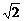 ∈(3,4),∴(
∈(3,4),∴(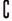 RA)∩B={4}.
RA)∩B={4}.
答案:D
1.(2004年全国Ⅱ,1)已知集合M={x|x2<4},N={x|x2-2x-3<0},则集合M∩N等于
A.{x|x<-2} B.{x|x>3} C.{x|-1<x<2} D.{x|2<x<3}
解析:M={x|x2<4}={x|-2<x<2},N={x|x2-2x-3<0}={x|-1<x<3},结合数轴,
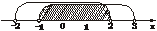
∴M∩N={x|-1<x<2}.
答案:C
3.集合的运算
(1)交集:由所有属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集,记为A∩B,即A∩B={x|x∈A且x∈B}.
(2)并集:由所有属于集合A或属于集合B的元素所组成的集合,叫做集合A与集合B的并集,记为A∪B,即A∪B={x|x∈A或x∈B}.
(3)补集:一般地,设S是一个集合,A是S的一个子集(即A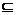 S),由S中所有不属于A的元素组成的集合,叫做子集A在全集S中的补集(或余集),记为
S),由S中所有不属于A的元素组成的集合,叫做子集A在全集S中的补集(或余集),记为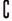 S A,即
S A,即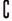 S A={x|x∈S且x
S A={x|x∈S且x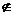 A}.
A}.
●点击双基
2.元素与集合、集合与集合之间的关系
(1)元素与集合:“∈”或“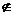 ”.
”.
(2)集合与集合之间的关系:包含关系、相等关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com