
2.掌握任意角的正弦、余弦、正切的定义,并会利用与单位圆有关的三角函数线表示正弦、余弦和正切;了解任意角的余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式.
1.理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算.
4.强化转化思想、方程思想的应用.
拓展题例
[例1] 杭州某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:
(1)引进该设备多少年后,开始盈利?
(2)引进该设备若干年后,有两种处理方案:
第一种:年平均盈利达到最大值时,以26万元的价格卖出;
第二种:盈利总额达到最大值时,以8万元的价格卖出.
问哪种方案较为合算?并说明理由.
解:(1)设引进设备n年后开始盈利,盈利为y万元,则y=50n-(12n+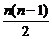 ×4)-98=-2n2+40n-98,由y>0,得10-
×4)-98=-2n2+40n-98,由y>0,得10-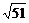 <n<10+
<n<10+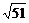 .
.
∵n∈N*,∴3≤n≤17,
即3年后开始盈利.
(2)方案一:年平均盈利为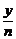 ,
,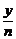 =-2n-
=-2n-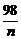 +40≤-2
+40≤-2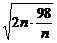 +40=12,
+40=12,
当且仅当2n=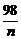 ,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
方案二:盈利总额y=-2(n-10)2+102,n=10时,y取最大值102,
即经过10年盈利总额最大,
共计盈利102+8=110万元.
两种方案获利相等,但由于方案二时间长,所以采用方案一合算.
[例2] 据某城市2002年末所作的统计资料显示,到2002年末,该城市堆积的垃圾已达50万吨,侵占了大量的土地,并且成为造成环境污染的因素之一.根据预测,从2003年起该城市还将以每年3万吨的速度产生新的垃圾,垃圾的资源化和回收处理已经成为该市城市建设中的重要问题.
(1)假设1992年底该城市堆积的垃圾为10万吨,从1993年到2002年这十年中,该城市每年产生的新垃圾以8%的年平均增长率增长,试求1993年该城市产生的新垃圾约有多少万吨?(精确到0.01,参考数据:1.0810≈2.159)
(2)如果从2003年起,该市每年处理上年堆积垃圾的20%,现有b1表示2003年底该市堆积的垃圾数量,b2表示2004年底该市堆积的垃圾数量……bn表示2002+n年底该城市堆积的垃圾数量,①求b1;②试归纳出bn的表达式(不用证明);③计算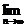 bn,并说明其实际意义.
bn,并说明其实际意义.
解:(1)设1993年该城市产生的新垃圾为x万吨.依题意,得
10+x+1.08x+1.082x+…+1.089x=50,
∴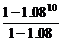 ·x=40.
·x=40.
∴x=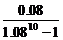 ×40≈2.76万吨.
×40≈2.76万吨.
∴1993年该城市产生的新垃圾约为2.76万吨.
(2)①b1=50×80%+3=43(万吨).
②∵b1=50×80%+3=50×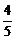 +3,
+3,
b2=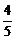 b1+3=50×(
b1+3=50×(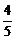 )2+3×
)2+3×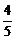 +3,
+3,
b3=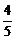 b2+3=50×(
b2+3=50×(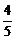 )3+3×(
)3+3×(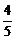 )2+3×
)2+3×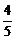 +3,
+3,
∴可归纳出bn=50×(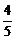 )n+3×(
)n+3×(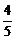 )n-1+3×(
)n-1+3×(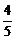 )n-2+…+3×
)n-2+…+3×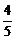 +3
+3
=50×(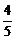 )n+3×
)n+3×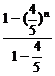 =50×(
=50×(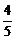 )n+15[1-(
)n+15[1-(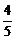 )n]=35×(
)n]=35×(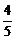 )n+15.
)n+15.
③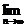 bn=
bn=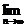 [35×(
[35×(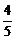 )n+15]=15.
)n+15]=15.
这说明,按题目设想的方法处理垃圾,该市垃圾总量将逐年减少,但不会少于15万吨.
3.“等额还款方式”采用“双向储蓄”的方法比较简便.
2.分期付款问题要弄清付款方式,不同方式抽象出的数学模型则不一样.
1.解应用题的关键是建立数学模型,转化为数学问题,要加强培养学生的转化意识.
3.数列的综合问题常与函数、方程、不等式等知识相互联系和渗透.
●教师下载中心
教学点睛
2.将实际问题转化为数列问题时应注意:
(1)分清是等差数列还是等比数列;
(2)分清是求an还是求Sn,特别要准确地确定项数n.
1.等差、等比数列的应用题常见于:产量增减、价格升降、细胞繁殖等问题,求利率、增长率等问题也常归结为数列建模问题.
8.(2004年春季北京,20)下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
… |
a1j |
… |
|
7 |
12 |
( ) |
( ) |
( ) |
… |
a2j |
… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
… |
a3j |
… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
… |
a4j |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
ai1 |
ai2 |
ai3 |
ai4 |
ai5 |
… |
aij |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
其中每行、每列都是等差数列,aij表示位于第i行第j列的数.
(1)写出a45的值;
(2)写出aij的计算公式;
(3)证明:正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
(1)解:a45=49.
(2)解:该等差数阵的第一行是首项为4,公差为3的等差数列:a1j=4+3(j-1),
第二行是首项为7,公差为5的等差数列:a2j=7+5(j-1),
……
第i行是首项为4+3(i-1),公差为2i+1的等差数列,
因此aij=4+3(i-1)+(2i+1)(j-1)=2ij+i+j=i(2j+1)+j.
(3)证明:必要性:若N在该等差数阵中,则存在正整数i、j使得N=i(2j+1)+j,
从而2N+1=2i(2j+1)+2j+1=(2i+1)(2j+1),
即正整数2N+1可以分解成两个不是1的正整数之积.
充分性:若2N+1可以分解成两个不是1的正整数之积,由于2N+1是奇数,则它必为两个不是1的奇数之积,即存在正整数k、l,使得2N+1=(2k+1)(2l+1),
从而N=k(2l+1)+l=akl,
可见N在该等差数阵中.
综上所述,正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com