
1.(2005年北京海淀区高三期末练习)函数y=xsinx+cosx在下面哪个区间内是增函数
A.(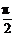 ,
, ) B.(π,2π)
) B.(π,2π)
C.( ,
,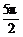 ) D.(2π,3π)
) D.(2π,3π)
解析:仿前面第3小题依次排除A、B、D.
答案:C
5.y=5sin(2x+θ)的图象关于y轴对称,则θ=_______.
解析:y=f(x)为偶函数.
答案:θ=kπ+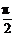 (k∈Z)
(k∈Z)
●典例剖析
[例1] 判断下面函数的奇偶性:
f(x)=lg(sinx+ ).
).
剖析:判断奇偶性首先应看定义域是否关于原点对称,然后再看f(x)与f(-x)的关系.
解:定义域为R,又f(x)+f(-x)=lg1=0,
即f(-x)=-f(x),∴f(x)为奇函数.
评述: 定义域关于原点对称是函数具有奇偶性的必要(但不充分)条件.
[例2] 求下列函数的单调区间:
(1)y= sin(
sin(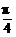 -
-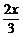 );(2)y=-|sin(x+
);(2)y=-|sin(x+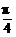 )|.
)|.
剖析:(1)要将原函数化为y=- sin(
sin(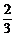 x-
x-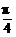 )再求之.(2)可画出y=-|sin(x+
)再求之.(2)可画出y=-|sin(x+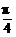 )|的图象.
)|的图象.
解:(1)y= sin(
sin(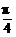 -
-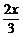 )=-
)=- sin(
sin(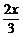 -
-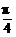 ).
).
故由2kπ-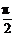 ≤
≤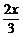 -
-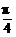 ≤2kπ+
≤2kπ+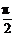
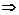 3kπ-
3kπ-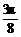 ≤x≤3kπ+
≤x≤3kπ+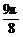 (k∈Z),为单调减区间;由2kπ+
(k∈Z),为单调减区间;由2kπ+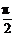 ≤
≤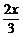 -
-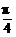 ≤2kπ+
≤2kπ+
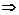 3kπ+
3kπ+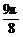 ≤x≤3kπ+
≤x≤3kπ+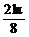 (k∈Z),为单调增区间.
(k∈Z),为单调增区间.
∴递减区间为[3kπ-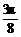 ,3kπ+
,3kπ+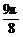 ],
],
递增区间为[3kπ+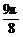 ,3kπ+
,3kπ+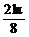 ](k∈Z).
](k∈Z).
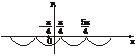
(2)y=-|sin(x+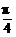 )|的图象的增区间为[kπ-
)|的图象的增区间为[kπ-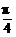 ,kπ+
,kπ+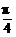 ],减区间为[kπ+
],减区间为[kπ+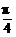 ,kπ+
,kπ+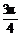 ].
].
深化拓展
(2)不用图象能求解吗?
提示:y=-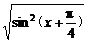 =-
=-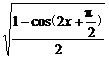 =-
=-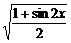 .
.
[例3] (2003年春季北京)已知函数f(x)=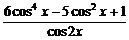 ,求f(x)的定义域,判断它的奇偶性,并求其值域.
,求f(x)的定义域,判断它的奇偶性,并求其值域.
剖析:此题便于入手,求定义域、判断奇偶性靠定义便可解决,求值域要对函数化简整理.
解:由cos2x≠0得2x≠kπ+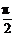 ,解得x≠
,解得x≠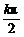 +
+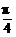 (k∈Z).
(k∈Z).
所以f(x)的定义域为{x|x∈R且x≠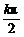 +
+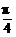 ,k∈Z}.
,k∈Z}.
因为f(x)的定义域关于原点对称,且
f(-x)=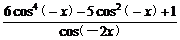
=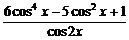 =f(x),
=f(x),
所以f(x)是偶函数.
又当x≠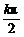 +
+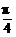 (k∈Z)时,
(k∈Z)时,
f(x)=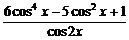 =
=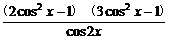 =3cos2x-1,
=3cos2x-1,
所以f(x)的值域为{y|-1≤y< 或
或 <y≤2}.
<y≤2}.
评述:本题主要考查三角函数的基本知识,考查逻辑思维能力、分析和解决问题的能力.
●闯关训练
夯实基础
4.(2004年全国Ⅱ,11)函数y=sin4x+cos2x的最小正周期为
A.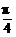 B.
B.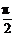 C.π D.2π
C.π D.2π
解析:y=sin4x+cos2x
=(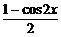 )2+
)2+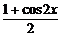
=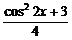 =
=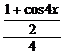 +
+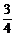
=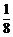 cos4x+
cos4x+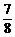 .
.
故最小正周期T=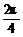 =
=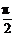 .
.
答案:B
3.(2004年全国Ⅱ,10)函数y=xcosx-sinx在下面哪个区间内是增函数
A.(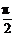 ,
, ) B.(π,2π)
) B.(π,2π)
C.( ,
,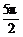 ) D.(2π,3π)
) D.(2π,3π)
解析:用排除法,可知B正确.
答案:B
2.(2004年天津,12)定义在R上的函数f(x)既是偶函数又是周期函数.若f(x)的最小正周期是π,且当x∈[0,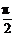 ]时,f(x)=sinx,则f(
]时,f(x)=sinx,则f(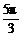 )的值为
)的值为
A.- B.
B. C.-
C.-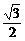 D.
D.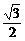
解析:f(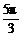 )=f(
)=f(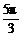 -2π)=f(-
-2π)=f(-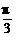 )=f(
)=f(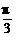 )=sin
)=sin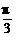 =
=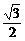 .
.
答案:D
1.(2003年春季上海)关于函数f(x)=sin2x-(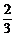 )|x|+
)|x|+ ,有下面四个结论,其中正确结论的个数为
,有下面四个结论,其中正确结论的个数为
①f(x)是奇函数 ②当x>2003时,f(x)> 恒成立 ③f(x)的最大值是
恒成立 ③f(x)的最大值是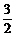 ④f(x)的最小值是-
④f(x)的最小值是-
A.1 B.2 C.3 D.4
解析:显然f(x)为偶函数,结论①错.
对于结论②,当x=1000π时,x>2003,sin21000π=0,∴f(1000π)= -(
-(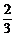 )1000π<
)1000π< ,因此结论②错.
,因此结论②错.
又f(x)=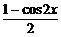 -(
-(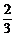 )|x|+
)|x|+ =1-
=1- cos2x-(
cos2x-(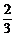 )|x|,-1≤cos2x≤1,
)|x|,-1≤cos2x≤1,
∴- ≤1-
≤1- cos2x≤
cos2x≤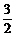 .
.
故1- cos2x-(
cos2x-(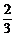 )|x|<
)|x|<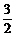 ,即结论③错.
,即结论③错.
而cos2x,(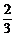 )|x|在x=0时同时取得最大值,所以f(x)=1-
)|x|在x=0时同时取得最大值,所以f(x)=1- cos2x-(
cos2x-(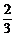 )|x|在x=0时可取得最小值-
)|x|在x=0时可取得最小值- ,即结论④是正确的.
,即结论④是正确的.
答案:A
2.能综合利用性质,并能解有关问题.
●点击双基
1.能利用“五点法”作三角函数的图象,并能根据图象求解析式.
4.7 三角函数的图象与性质(三)
●知识梳理
由1≤f(x)≤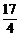
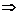 1≤-(sinx-
1≤-(sinx-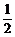 )2+a+
)2+a+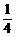 ≤
≤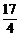
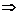 a-4≤(sinx-
a-4≤(sinx-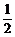 )2≤a-
)2≤a-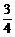 . ①
. ①
由-1≤sinx≤1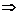 -
-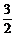 ≤sinx-
≤sinx-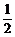 ≤
≤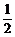
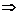 (sinx-
(sinx-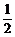 )
)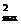 =
=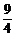 ,(sinx-
,(sinx-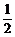 )
)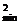 =0.
=0.
∴要使①式恒成立,
只需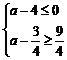
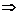 3≤a≤4.
3≤a≤4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com