
2.(2003年河南调研题)将函数y=2sin2x的图象按向量a平移,得到函数y=2sin(2x+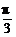 )+1的图象,则a等于
)+1的图象,则a等于
A.(-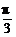 ,1) B.(-
,1) B.(-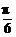 ,1)
,1)
C.(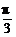 ,-1) D.(
,-1) D.(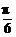 ,1)
,1)
解析:由y=2sin(2x+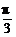 )+1得y=2sin2(x+
)+1得y=2sin2(x+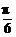 )+1,∴a=(-
)+1,∴a=(-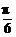 ,1).
,1).
答案:B
1.(2004年福州质量检查题)将函数y=sinx按向量a=(-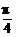 ,3)平移后的函数解析式为
,3)平移后的函数解析式为
A.y=sin(x-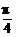 )+3 B.y=sin(x-
)+3 B.y=sin(x-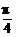 )-3
)-3
C.y=sin(x+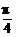 )+3 D.y=sin(x+
)+3 D.y=sin(x+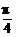 )-3
)-3
解析:由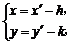 得
得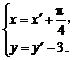
∴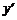 -3=sin(
-3=sin(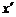 +
+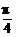 ).
).
∴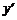 =sin(
=sin(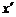 +
+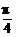 )+3,
)+3,
即y=sin(x+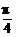 )+3.
)+3.
答案:C
5.(理)若△ABC的三边的中点坐标为(2,1)、(-3,4)、(-1,-1),则△ABC的重心坐标为____________.
解析:设A(x1,y1),B(x2,y2),C(x3,y3),
则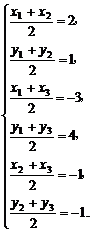 ∴
∴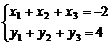
∴重心坐标为(-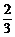 ,
,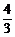 ).
).
答案:(-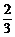 ,
,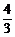 )
)
(文)已知点M1(6,2)和M2(1,7),直线y=mx-7与线段M1M2的交点M分有向线段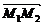 的比为3∶2,则m的值为____________.
的比为3∶2,则m的值为____________.
解析:设M(x,y),则x=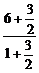 =
=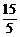 =3,y=
=3,y=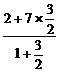 =
=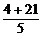 =5,即M(3,5),代入y=mx-7得5=3m-7,∴m=4.
=5,即M(3,5),代入y=mx-7得5=3m-7,∴m=4.
答案:4
●典例剖析
[例1] 已知点A(-1,6)和B(3,0),在直线AB上求一点P,使|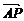 |=
|=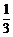 |
|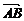 |.
|.
剖析:|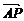 |=
|=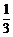 |
|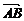 |,则
|,则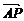 =
=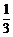
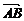 或
或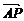 =
=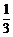
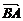 .设出P(x,y),向量转化为坐标运算即可.
.设出P(x,y),向量转化为坐标运算即可.
解:设P的坐标为(x,y),若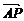 =
=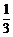
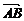 ,则由(x+1,y-6)=
,则由(x+1,y-6)=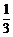 (4,-6),得
(4,-6),得
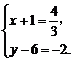 解得
解得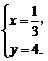
此时P点坐标为(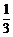 ,4).
,4).
若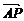 =-
=-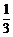
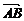 ,则由(x+1,y-6)=-
,则由(x+1,y-6)=-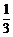 (4,-6)得
(4,-6)得
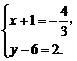 解得
解得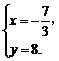
∴P(-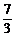 ,8).综上所述,P(
,8).综上所述,P(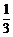 ,4)或(-
,4)或(-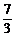 ,8).
,8).
深化拓展
本题亦可转化为定比分点处理.由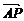 =
=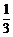
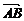 ,得
,得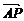 =
=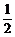
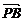 ,则P为
,则P为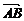 的定比分点,λ=
的定比分点,λ=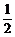 ,代入公式即可;若
,代入公式即可;若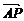 =-
=-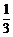
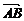 ,则
,则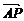 =-
=-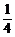
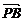 ,则P为
,则P为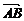 的定比分点,λ=-
的定比分点,λ=-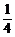 .
.

由两种方法比较不难得出向量的运算转化为坐标运算,是解决向量问题的一般方法.
[例2] 已知△ABC的三个顶点坐标分别是A(4,1),B(3,4),C(-1,2),BD是∠ABC的平分线,求点D的坐标及BD的长.
剖析:∵A、C两点坐标为已知,∴要求点D的坐标,只要能求出D分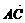 所成的比即可.
所成的比即可.
解:∵|BC|=2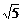 ,|AB|=
,|AB|=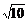 ,∴D分
,∴D分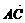 所成的比λ=
所成的比λ=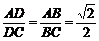 .
.
由定比分点坐标公式,得

∴D点坐标为(9-5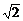 ,
,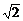 ).
).
∴|BD|=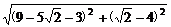 =
=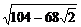 .
.
评述:本题给出了三点坐标,因此三边长度易知,由角平分线的性质通过定比分点可解出D点坐标,适当利用平面几何知识,可以使有些问题得以简化.
深化拓展
本题也可用如下解法:设D(x,y),∵BD是∠ABC的平分线,
∴〈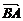 ,
,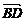 〉=〈
〉=〈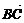 ,
,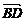 〉.
〉.
∴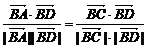 ,
,
即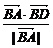 =
=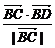 .
.
又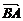 =(1,-3),
=(1,-3),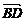 =(x-3,y-4),
=(x-3,y-4),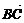 =(-4,-2),
=(-4,-2),
∴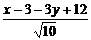 =
=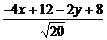 .
.
∴(4+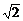 )x+(2-3
)x+(2-3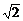 )y+9
)y+9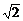 -20=0. ①
-20=0. ①
又A、D、C三点共线,∴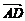 ,
,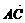 共线.
共线.
又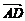 =(x-4,y-1),
=(x-4,y-1),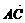 =(x+1,y-2),
=(x+1,y-2),
∴(x-4)(y-2)=(x+1)(y-1). ②
由①②可解得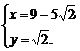
∴D点坐标为(9-5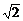 ,
,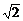 ),|BD|=
),|BD|=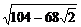 .
.
思考讨论
若BD是AC边上的高,或BD把△ABC分成面积相等的两部分,本题又如何求解?请读者思考.
[例3] 已知在□ABCD中,点A(1,1),B(2,3),CD的中点为E(4,1),将
□ABCD按向量a平移,使C点移到原点O.
(1)求向量a;
(2)求平移后的平行四边形的四个顶点的坐标.
解:(1)由□ABCD可得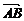 =
=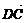 ,
,
设C(x3,y3),D(x4,y4),
则
又CD的中点为E(4,1),
则
由①-④得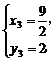
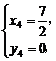
即C(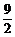 ,2),D(
,2),D(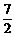 ,0).
,0).
∴a=(-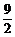 ,-2).
,-2).
(2)由平移公式得A′(-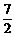 ,-1),B′(-
,-1),B′(-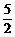 ,1),C′(0,0),D′(-1,-2).
,1),C′(0,0),D′(-1,-2).
●闯关训练
夯实基础
4.若点P分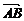 所成的比是λ(λ≠0),则点A分
所成的比是λ(λ≠0),则点A分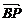 所成的比是____________.
所成的比是____________.
解析:∵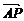 =λ
=λ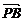 ,∴
,∴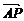 =λ(-
=λ(-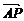 +
+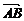 ).∴(1+λ)
).∴(1+λ)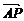 =λ
=λ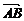 .
.
∴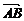 =
=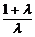
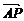 .∴
.∴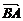 =-
=-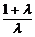
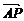 .
.
答案:-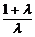
3.设A、B、C三点共线,且它们的纵坐标分别为2、5、10,则A点分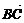 所得的比为
所得的比为
A.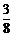 B.
B.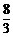
C.-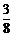 D.-
D.-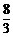
解析:设A点分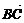 所得的比为λ,则由2=
所得的比为λ,则由2=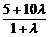 ,得λ=-
,得λ=-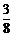 .
.
答案:C
2.(2004年湖北八校第二次联考)将抛物线y2=4x沿向量a平移得到抛物线y2-4y=4x,则向量a为
A.(-1,2) B.(1,-2)
C.(-4,2) D.(4,-2)
解析:设a=(h,k),由平移公式得
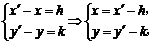
代入y2=4x得
(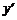 -k)2=4(
-k)2=4(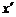 -h),
-h),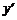 2-2k
2-2k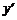 =4
=4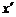 -4h-k2,
-4h-k2,
即y2-2ky=4x-4h-k2,
∴k=2,h=-1.
∴a=(-1,2).
答案:A
思考讨论
本题不用平移公式代入配方可以吗?
提示:由y2-4y=4x,配方得
(y-2)2=4(x+1),
∴h=-1,k=2.(知道为什么吗?)
1.(2004年东北三校联考题)若将函数y=f(x)的图象按向量a平移,使图象上点的坐标由(1,0)变为(2,2),则平移后的图象的解析式为
A.y=f(x+1)-2 B.y=f(x-1)-2
C.y=f(x-1)+2 D.y=f(x+1)+2
解析:由平移公式得a=(1,2),则平移后的图象的解析式为y=f(x-1)+2.
答案:C
3.定比分点的应用:利用定比分点可证共线问题.
●点击双基
2.定比分点的向量表达式:
P点分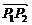 成的比为λ,则
成的比为λ,则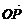 =
=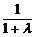
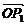 +
+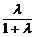
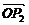 (O为平面内任一点).
(O为平面内任一点).
1.定比分点的定义:点P为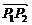 所成的比为λ,用数学符号表达即为
所成的比为λ,用数学符号表达即为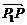 =λ
=λ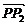 .当λ>0时,P为内分点;λ<0时,P为外分点.
.当λ>0时,P为内分点;λ<0时,P为外分点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com