
1.复习不等式的性质时,要克服“想当然”和“显然成立”的思维定势,要以比较准则和实数的运算法则为依据.
5.理解不等式|a|-|b|≤|a±b|≤|a|+|b|.
●复习方略指南
本章内容在高考中,以考查不等式的性质、证明、解法和最值方面的应用为重点,多数是与函数、方程、三角、数列、几何综合在一起被考查,单独考查不等式的问题较少,尤其是不等式的证明题.
借助不等式的性质及证明,主要考查函数方程思想、等价转化思想、数形结合思想及分类讨论思想等数学思想方法.含参数不等式的解法与讨论,不等式与函数、数列、三角等内容的综合问题,仍将是今后高考命题的热点.
本章内容理论性强,知识覆盖面广,因此复习中应注意:
4.掌握不等式的解法.
3.掌握比较法、分析法、综合法证明简单的不等式.
2.掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单地应用.
1.理解不等式的性质及应用.
9.如下图,已知△OFQ的面积为S,且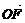 与
与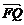 的数量积等于1,
的数量积等于1,

(1)若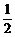 <S<2,求向量
<S<2,求向量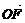 与
与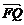 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设|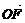 |=c(c≥2),S=
|=c(c≥2),S=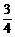 c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当| |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
解:(1)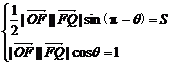
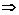 tanθ=2S.又∵
tanθ=2S.又∵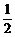 <S<2,
<S<2,
∴1<tanθ<4.∴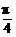 <θ<arctan4.
<θ<arctan4.
(2)以O为原点,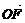 所在直线为x轴建立坐标系,
所在直线为x轴建立坐标系,
设椭圆方程为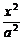 +
+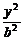 =1(a>b>0),
=1(a>b>0),
点Q(x1,y1),则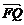 =(x1-c,y1).
=(x1-c,y1).
又∵△OFQ的面积为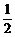 |
|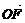 |·y1=
|·y1=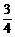 c,
c,
∴y1=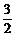 .又由
.又由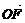 ·
·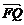 =1,解得x1=c+
=1,解得x1=c+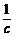 .
.
| |=
|=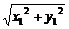 =
= (c≥2).
(c≥2).
设f(c)=c+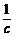 ,则
,则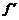 (c)=1-
(c)=1-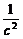 =
=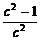 .
.
当c≥2时,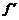 (c)>0,∴f(c)在[2,+∞)上递增,∴当c=2时,|
(c)>0,∴f(c)在[2,+∞)上递增,∴当c=2时,| |最小,
|最小,
此时Q(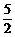 ,
,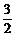 ),由此可得
),由此可得
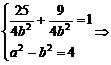 a2=10,b2=6.
a2=10,b2=6.
∴椭圆方程为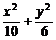 =1.
=1.
●思悟小结
向量兼具代数的抽象与严谨和几何的直观,向量本身是一个数形结合的产物,因此在向量的复习中要注意数与形的结合、代数与几何的结合、形象思维与逻辑思维的结合.应用向量可以解决平面几何中的一些问题,在物理和工程技术中应用也很广泛.
●教师下载中心
教学点睛
教材中安排了解三角形应用举例和实习作业,根据新教材突出应用这一显著特点,教学中应充分利用这些素材,使学生受到把实际问题抽象成数学问题的训练,渗透数学建模思想,培养学生分析、解决实际问题的能力.
拓展题例
[例1] 已知a=( x2,x),b=(x,x-3),x∈[-4,4].
x2,x),b=(x,x-3),x∈[-4,4].
(1)求f(x)=a·b的表达式;
(2)求f(x)的最小值,并求此时a与b的夹角.
解:(1)f(x)=a·b= x2·x+x·(x-3)=
x2·x+x·(x-3)= x3+x2-3x,x∈[-4,4].
x3+x2-3x,x∈[-4,4].
(2)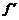 (x)=x2+2x-3=(x+3)(x-1).
(x)=x2+2x-3=(x+3)(x-1).
列表:
|
x |
-4 |
(-4,-3) |
-3 |
(-3,1) |
1 |
(1,4) |
4 |
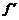 (x) (x) |
|
+ |
0 |
- |
0 |
+ |
|
|
f(x) |
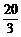 |
↑ |
极大值9 |
↓ |
极小值-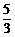 |
↑ |
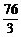 |
故当x=1时,f(x)有最小值为-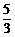 .
.
此时a=( ,1),b=(1,-2).
,1),b=(1,-2).
设θ为a与b的夹角,则cosθ=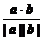 =-
=-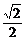 .
.
又由θ∈[0,π],得θ= .
.
[例2] 如图所示,对于同一高度(足够高)的两个定滑轮,用一条(足够长)绳子跨过它们,并在两端分别挂有4 kg和2 kg的物体,另在两个滑轮中间的一段绳子悬挂另一物体,为使系统保持平衡状态,此物体的质量应是多少?(忽略滑轮半径、绳子的重量)
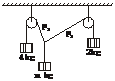
分析:先进行受力分析,列出平衡方程,然后用数学方法求解.
解:设所求物体质量为m kg时,系统保持平衡,再设F1与竖直方向的夹角为θ1,F2与竖直方向的夹角为θ2,则有

(其中g为重力加速度).
由①式和②式消去θ2,得
m2-8mcosθ1+12=0,
即m=4cosθ1±2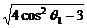 . ③
. ③
∵cosθ2>0,由②式知,③式中m=4cosθ1-2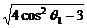 不合题意,舍去.
不合题意,舍去.
又∵4cos2θ1-3≥0,解得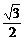 ≤cosθ1≤1.
≤cosθ1≤1.
经检验,当cosθ1=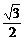 时,cosθ2=0,不合题意,舍去.
时,cosθ2=0,不合题意,舍去.
∴2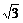 <m<6.
<m<6.
综上,所求物体的质量在2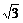 kg到6 kg之间变动时,系统可保持平衡.
kg到6 kg之间变动时,系统可保持平衡.
评注:(1)m的范围是通过函数y=4x+2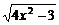 的单调性求得的.(2)实际问题的处理要注意变量的实际意义,本题容易忽略cosθ2>0的实际限制.
的单调性求得的.(2)实际问题的处理要注意变量的实际意义,本题容易忽略cosθ2>0的实际限制.
8.如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
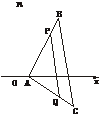
解:设P分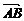 的比为λ1,则
的比为λ1,则
4=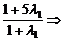 λ1=3,
λ1=3,
即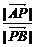 =3,
=3,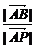 =
=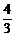 .
.
又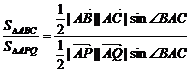
=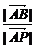 ·
· =
=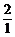 ,
,
∴ =
=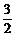 ,即
,即 =2.
=2.
设λ2=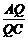 ,则λ2=2.∴xQ=
,则λ2=2.∴xQ=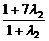 =5,
=5,
yQ=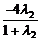 =-
=-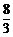 .∴Q(5,-
.∴Q(5,-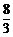 ).
).
探究创新
7.已知A(4,0),N(1,0),若点P满足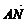 ·
·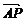 =6|
=6|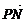 |.
|.
(1)求点P的轨迹方程,并说明该轨迹是什么曲线;
(2)求|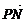 |的取值范围;
|的取值范围;
(3)若M(-1,0),求∠MPN在[0,π]上的取值范围.
解:(1)设P(x,y),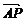 =(x-4,y),
=(x-4,y),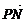 =(1-x,-y),
=(1-x,-y),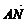 =(-3,0),∵
=(-3,0),∵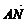 ·
·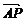 =6|
=6|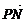 |,
|,
∴-3(x-4)=6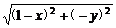 ,即3x2+4y2=12.
,即3x2+4y2=12.
∴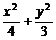 =1.∴P点的轨迹是以(-1,0)、(1,0)为焦点,长轴长为4的椭圆.
=1.∴P点的轨迹是以(-1,0)、(1,0)为焦点,长轴长为4的椭圆.
(2)N(1,0)为椭圆的右焦点,x=4为右准线,设P(x0,y0),P到右准线的距离为d,d=4-x0,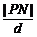 =e=
=e=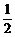 ,|PN|=
,|PN|=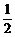 d=
d=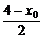 .∵-2≤x0≤2,∴1≤|PN|≤3.
.∵-2≤x0≤2,∴1≤|PN|≤3.
当|PN|=1时,P(2,0);当|PN|=3时,P(-2,0).
(3)令|PN|=t(1≤t≤3),
则|PM|=4-t,|MN|=2,
cos∠MPN=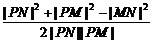 =
=
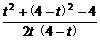 =-1+
=-1+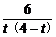 .
.
由1≤t≤3,得3≤t(4-t)≤4,
∴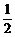 ≤cos∠MPN≤1.∴0≤∠MPN≤
≤cos∠MPN≤1.∴0≤∠MPN≤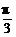 .
.
6.如图,用两根绳子把重10 N的物体W吊在水平杆子AB上.∠ACW=150°,∠BCW=120°,求A和B处所受力的大小.(忽略绳子重量)
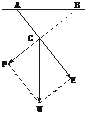
解:设A、B处所受力分别为f1、f2,10 N的重力用f表示,则f1+f2=f.以重力作用点C为f1、f2的始点,作平行四边形CFWE,使CW为对角线,则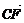 =f1,
=f1,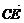 =f2,
=f2,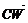 =f,则∠ECW=180°-150°=30°,
=f,则∠ECW=180°-150°=30°,
∠FCW=180°-120°=60°,∠FCE=90°.
∴四边形CEWF为矩形.
∴|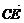 |=|
|=|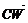 |cos30°=10·
|cos30°=10·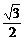 =5
=5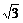 ,
,
|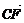 |=|
|=|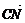 |cos60°=10×
|cos60°=10×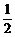 =5.
=5.
∴A处受力为5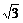 N,B处受力为5 N.
N,B处受力为5 N.
培养能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com