
3.方程2sin2x=x-3的解的个数为_______.
解析:画图象.
答案:3
2.(2004年全国Ⅰ,9)为了得到函数y=sin(2x-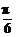 )的图象,可以将函数y=cos2x的图象
)的图象,可以将函数y=cos2x的图象
A.向右平移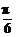 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度
C.向左平移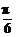 个单位长度 D.向左平移
个单位长度 D.向左平移 个单位长度
个单位长度
解析:∵y=sin(2x-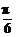 )=cos[
)=cos[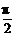 -(2x-
-(2x-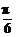 )]=cos(
)]=cos(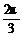 -2x)=cos(2x-
-2x)=cos(2x-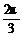 )=
)=
cos[2(x- )],
)],
∴将函数y=cos2x的图象向右平移 个单位长度.
个单位长度.
答案:B
1.(2004年辽宁,7)已知函数f(x)=sin(πx-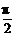 )-1,则下列命题正确的是
)-1,则下列命题正确的是
A.f(x)是周期为1的奇函数
B.f(x)是周期为2的偶函数
C.f(x)是周期为1的非奇非偶函数
D.f(x)是周期为2的非奇非偶函数
解析:T=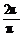 =2,且f(x)=sin(πx-
=2,且f(x)=sin(πx-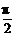 )-1=cos2x-1,∴f(x)为偶函数.
)-1=cos2x-1,∴f(x)为偶函数.
答案:B
5.(2004年全国,5)已知函数y=tan(2x+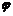 )的图象过点(
)的图象过点(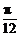 ,0),则
,0),则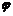 可以是
可以是
A.-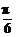 B.
B.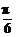 C.-
C.-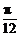 D.
D.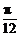
解析:将(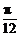 ,0)代入原函数可得,tan(
,0)代入原函数可得,tan(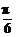 +
+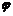 )=0,再将A、B、C、D代入检验即可.
)=0,再将A、B、C、D代入检验即可.
答案:A
●典例剖析
[例1] 把函数y=cos(x+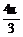 )的图象向左平移4个单位,所得的函数为偶函数,则
)的图象向左平移4个单位,所得的函数为偶函数,则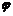 的最小值是
的最小值是
A.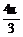 B.
B.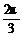 C.
C. D.
D.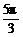
剖析:先写出向左平移4个单位后的解析式,再利用偶函数的性质求解.
向左平移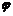 个单位后的解析式为y=cos(x+
个单位后的解析式为y=cos(x+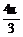 +
+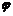 ),
),
则cos(-x+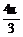 +
+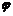 )=cos(x+
)=cos(x+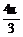 +
+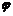 ),
),
cosxcos(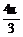 +
+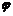 )+sinxsin(
)+sinxsin(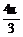 +
+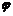 )
)
=cosxcos(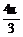 +
+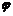 )-sinxsin(
)-sinxsin(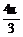 +
+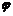 ).
).
∴sinxsin(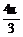 +
+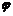 )=0,x∈R.
)=0,x∈R.
∴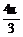 +
+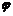 =kπ.∴
=kπ.∴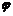 =kπ-
=kπ-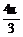 >0.
>0.
∴k>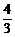 .∴k=2.∴
.∴k=2.∴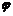 =
=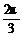 .
.
答案:B
[例2] 试述如何由y=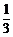 sin(2x+
sin(2x+ )的图象得到y=sinx的图象.
)的图象得到y=sinx的图象.
解:y=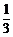 sin(2x+
sin(2x+ )
)
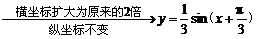
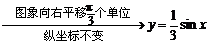

深化拓展
还有其他变换吗?不妨试一试.
答案:(1)先将y=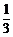 sin(2x+
sin(2x+ )的图象向右平移
)的图象向右平移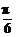 个单位,得y=
个单位,得y=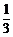 sin2x的图象;
sin2x的图象;
(2)再将y=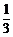 sin2x上各点的横坐标扩大为原来的2倍(纵坐标不变),得y=
sin2x上各点的横坐标扩大为原来的2倍(纵坐标不变),得y=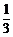 sinx的图象;
sinx的图象;
(3)再将y=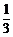 sinx图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到y=sinx的图象.
sinx图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到y=sinx的图象.
[例3] (2004年重庆,17)求函数y=sin4x+2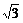 sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.
sinxcosx-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.
解:y=sin4x+2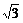 sinxcosx-cos4x
sinxcosx-cos4x
=(sin2x+cos2x)(sin2x-cos2x)+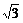 sin2x
sin2x
=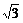 sin2x-cos2x
sin2x-cos2x
=2sin(2x-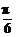 ).
).
故该函数的最小正周期是π;最小值是-2;单调递增区间是[0, ],[
],[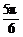 ,π].
,π].
评述:把三角函数式化简为y=Asin(ωx+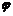 )+k(ω>0)是解决周期、最值、单调区间问题的常用方法.
)+k(ω>0)是解决周期、最值、单调区间问题的常用方法.
●闯关训练
夯实基础
4.设函数f(x)=A+Bsinx,若B<0时,f(x)的最大值是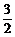 ,最小值是-
,最小值是-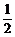 ,则A=_______,B=_______.
,则A=_______,B=_______.
解析:根据题意,由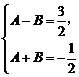 可得结论.
可得结论.
答案: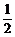 -1
-1
3.(2005年春季北京,4)如果函数f(x)=sin(πx+θ)(0<θ<2π)的最小正周期是T,且当x=2时取得最大值,那么
A.T=2,θ=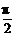 B.T=1,θ=π
B.T=1,θ=π
C.T=2,θ=π D.T=1,θ=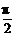
解析:T=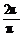 =2,又当x=2时,sin(π·2+θ)=sin(2π+θ)=sinθ,要使上式取得最大值,可取θ=
=2,又当x=2时,sin(π·2+θ)=sin(2π+θ)=sinθ,要使上式取得最大值,可取θ=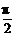 .
.
答案:A
2.(2002年全国)在(0,2π)内,使sinx>cosx成立的x的取值范围是
A.(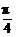 ,
,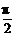 )∪(π,
)∪(π,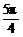 ) B.(
) B.(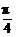 ,π)
,π)
C.(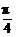 ,
,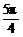 ) D.(
) D.(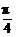 ,π)∪(
,π)∪(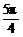 ,
, )
)
解析:利用三角函数线.
答案:C
1.(2002年全国)函数y=-xcosx的部分图象是
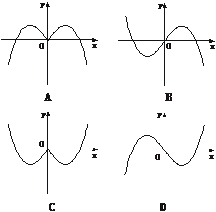
解析:y=-xcosx为奇函数,且当x0+时,图象在x轴下方.
答案:D
3.给出图象确定解析式y=Asin(ωx+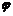 )的题型,有时从寻找“五点”中的第一零点(-
)的题型,有时从寻找“五点”中的第一零点(-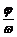 ,0)作为突破口,要从图象的升降情况找准第一个零点的位置.
,0)作为突破口,要从图象的升降情况找准第一个零点的位置.
●点击双基
2.利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现.无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com