
题目列表(包括答案和解析)
5. 将7名学生分配到甲、乙两个宿舍,每个宿舍至少安排2名学生,那么互不相同的安
将7名学生分配到甲、乙两个宿舍,每个宿舍至少安排2名学生,那么互不相同的安
 排方法的种数为( )
排方法的种数为( )
 A.72
B.120
C.
252
D. 112
A.72
B.120
C.
252
D. 112
4. 设m、n是不同的直线,
设m、n是不同的直线,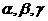 是不同的平面,有以下四个命题
是不同的平面,有以下四个命题
 ①
①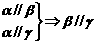 ;②
;②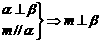 ;③
;③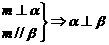 ;④
;④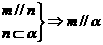
 其中为真命题的是 ( )
其中为真命题的是 ( )
 A.①④ B.①③ C.②③ D.②④
A.①④ B.①③ C.②③ D.②④
3. 若
若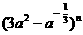 的展开式中含有常数项,则正整数n的最小值是( )
的展开式中含有常数项,则正整数n的最小值是( )
 A.
5
B. 6
C. 7
D. 8
A.
5
B. 6
C. 7
D. 8
2. 袋中装有4个红球和3个黄球,从中任取4个球,则既有红球又有黄球的不同取法有( ). A.34种 B.
35种
C. 120种
D. 140种
袋中装有4个红球和3个黄球,从中任取4个球,则既有红球又有黄球的不同取法有( ). A.34种 B.
35种
C. 120种
D. 140种
1. 集合
集合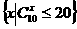 中元素个数为( )
中元素个数为( )
 A.2个 B.3个
C.4个
D.5个
A.2个 B.3个
C.4个
D.5个
21.(12分)已知直线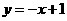 与椭圆
与椭圆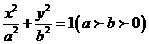 相交于A、B两点,且线段AB的中点在直线
相交于A、B两点,且线段AB的中点在直线 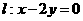 上
上
(1) 求此椭圆的离心率;
(2) 若椭圆的右焦点关于直线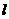 的对称点在圆
的对称点在圆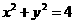 上,求此椭圆的方程。
上,求此椭圆的方程。
20.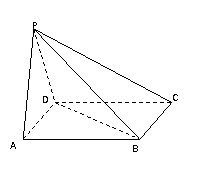 (10分)如图,在四棱锥
(10分)如图,在四棱锥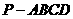 中,底面
中,底面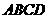 是正方形,侧面
是正方形,侧面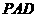 是正三角形,
是正三角形,
且平面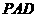
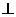 底面
底面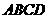 .
.
(1)求证:平面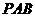
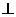 平面
平面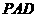 ;
;
(2)求二面角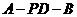 的大小;
的大小;
(3)设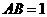 ,求点
,求点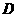 到平面
到平面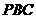 的距离.
的距离.
19. (10分)已知等差数列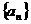 的首项
的首项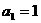 ,公差
,公差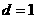 ,前
,前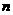 项和为
项和为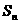 ,
,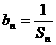 ,
,
(1)求数列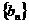 的通项公式;
的通项公式;
(2)求证: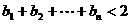
18.(10分)9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为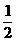 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
(Ⅰ)求甲坑不需要补种的概率;
(Ⅱ)求3个坑中恰有1个坑不需要补种的概率;
(Ⅲ)求有坑需要补种的概率。
17.(10分)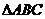 中,内角
中,内角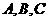 的对边分别为
的对边分别为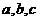 ,且
,且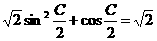 .
.
(1)求角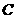 的大小;(2)若
的大小;(2)若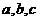 成等比数列,求
成等比数列,求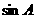 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com