
题目列表(包括答案和解析)
5.在平面直角坐标平面上,不等式组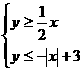 所表示的平面区域的面积等于 ( )
所表示的平面区域的面积等于 ( )
A.6 B.9 C.12 D.15
4.已知α、β、γ表示平面,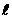 、K表示直线,并且有
、K表示直线,并且有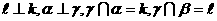 。给出三个结论:①
。给出三个结论:①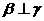 ;②
;②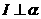 ;③
;③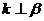 。其中正确的结论的个数是 ( )
。其中正确的结论的个数是 ( )
A.0 B.1 C.2 D.3
3.命题甲:p是q 的充分条件;命题乙:p是q的充分必要条件。则命题甲是命题乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.(理科)已知复数z和(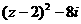 都是纯虚数,则z= ( )
都是纯虚数,则z= ( )
A.i B.-2i C.-i D.2i
(文科)函数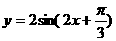 的初相为 ( )
的初相为 ( )
A.-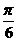 B.-
B.-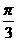 C.
C.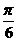 D.
D.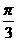
1.满足条件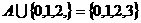 的所有集合A的个数是 ( )
的所有集合A的个数是 ( )
A.6 B.7 C.8 D.16
22.(14分)
椭圆G: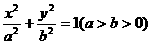 的两个焦点F1(-c,0),F2(c,0),M是椭圆上一点,且满足
的两个焦点F1(-c,0),F2(c,0),M是椭圆上一点,且满足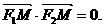
(1)求椭圆的离心率e的取值范围;
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为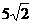 。
。
①求此时椭圆G的方程;
②(理)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB中点,问A、B两点能否关于过点P(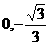 )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
21.(12分)设 的整数部分。
的整数部分。
(1)求F(1)、F(2)、F(3);
(2)求满足F(m)=3的m的值;
(3)(文)求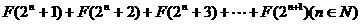
(理)求证:F(1)+F(2)+F(3)+…+F(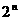 )=(n-2)·2n+n+2 (n∈N)
)=(n-2)·2n+n+2 (n∈N)
20.(12分)
如图,正四棱柱ABCD-A1B1C1D1的底面边长是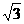 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
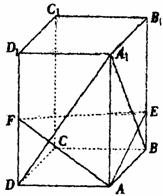 (1)求证:A1C⊥平面AEF;
(1)求证:A1C⊥平面AEF;
(2)求二面角A-EF-B的大小?
(3)求点B1到平面AEF的距离?
19.(12分)
袋中有4个红球,3个黑球,今从袋中随机取出4个球,设取到一个红球得2分,取到一个黑球得1分。
(1)(文)求可能得分ξ的取值及相应的概率;
(2)(理)求得分ξ的概率分布和数学期望。
18.(12分)
已知函数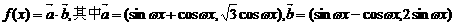
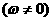 ,若
,若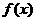 相邻两对称轴间的距离不小于1,求ω的最大值。
相邻两对称轴间的距离不小于1,求ω的最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com