
题目列表(包括答案和解析)
8.(2003年杭州市质检题)当a≠0时,函数y=ax+b和y=bax的图象只可能是
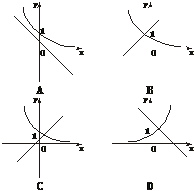
答案:C
7.F(x)=(1+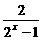 )·f(x)(x≠0)是偶函数,且f(x)不恒等于零,则f(x)
)·f(x)(x≠0)是偶函数,且f(x)不恒等于零,则f(x)
A.是奇函数 B.是偶函数
C.既是奇函数,又是偶函数 D.是非奇非偶函数
解析:g(x)=1+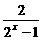 是奇函数,
是奇函数,
∴f(x)是奇函数.
答案:A
6.(2004年江苏,11)设k>1,f(x)=k(x-1)(x∈R),在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A点,它的反函数y=f-1(x)的图象与y轴交于B点,且这两个函数的图象交于P点.已知四边形OAPB的面积是3,则k等于
A.3 B.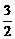 C.
C.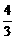 D.
D.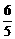
解析:用k表示出四边形OAPB的面积.
答案:B
5.函数f(x)是一个偶函数,g(x)是一个奇函数,且f(x)+g(x)=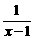 ,则f(x)等于
,则f(x)等于
A.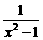 B.
B.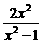 C.
C.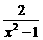 D.
D.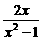
解析:由题知f(x)+g(x)=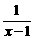 , ①
, ①
以-x代x,①式得f(-x)+g(-x)=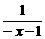 ,即f(x)-g(x)=
,即f(x)-g(x)=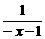 , ②
, ②
①+②得f(x)=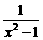 .
.
答案:A
4.(2004年上海,文15)若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则f(x)等于
A.10x-1 B.1-10x
C.1-10-x D.10-x-1
解析:∵y=f(x)与y=lg(x+1)关于x-y=0对称,
∴y=f(x)与y=lg(x+1)互为反函数.
∴由y=lg(x+1),得x=10y-1.
∴所求y=f(x)=10x-1.
答案:A
3.f(x)是定义在R上的奇函数,它的最小正周期为T,则f(-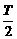 )的值为
)的值为
A.0 B.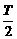 C.T D.-
C.T D.-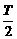
解法一:由f(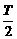 )=f(-
)=f(-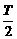 +T)=f(-
+T)=f(-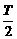 )=-f(
)=-f(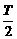 ),知f(
),知f(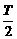 )=0.
)=0.
解法二:取特殊函数f(x)=sinx.
答案:A
2.(2004年全国Ⅲ,理11)设函数f(x)=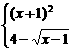
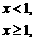 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
解析:当x<1时,f(x)≥1 (x+1)2≥1
(x+1)2≥1 x≤-2或x≥0,∴x≤-2或0≤x<1.
x≤-2或x≥0,∴x≤-2或0≤x<1.
当x≥1时,f(x)≥1 4-
4-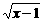 ≥1
≥1
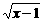 ≤3
≤3 1≤x≤10.
1≤x≤10.
综上,知x≤-2或0≤x≤10.
答案:A
1.(2002年全国)函数y=x2+bx+c(x∈[0,+∞))是单调函数的充要条件是
A.b≥0 B.b≤0
C.b>0 D.b<0
解析:y=x2+bx+c的对称轴为x=-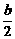 ,∴-
,∴-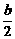 ≤0.∴b≥0.
≤0.∴b≥0.
答案:A
22.(14分)设坐标平面上全部向量的集合为V,a=(a1,a2)为V的一个单位向量.已知从V到V的映射f由f(x)=-x+2(x·a)a(x∈V)确定.
(1)若x、y∈V,求证:f(x)·f(y)=x·y;
(2)对于x∈V,计算f[f(x)]-x;
(3)设u=(1,0),v=(0,1),若f(u)=v,求a.
(1)证明:f(x)·f(y)=[-x+2(x·a)a]·[-y+2(y·a)a]
=x·y-4(x·a)(y·a)+4(x·a)(y·a)a2=x·y.
(2)解:∵f[f(x)]=f[-x+2(x·a)a]
=-[-x+2(x·a)a]+2{[-x+2(x·a)a]·a}a
=x-2(x·a)a+2[-x·a+2(x·a)a2]a
=x-2(x·a)a+2(x·a)a=x,
∴f[f(x)]-x=0.
(3)解:由f(u)=v,得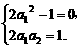
解得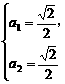 或
或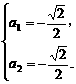
∴a=(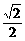 ,
,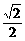 )或a=(-
)或a=(-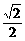 ,-
,-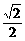 ).
).
21.(12分)已知矩形ABCD,E、F分别是AD、BC的中点,求证:对角线AC⊥BE,AC⊥DF的充要条件是AB∶BC=1∶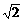 .
.
证明:设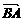 =a,
=a,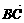 =b,则a⊥b.
=b,则a⊥b.
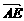 =
=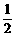 b,
b,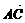 =b-a,
=b-a,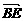 =
=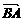 +
+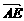 =a+
=a+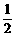 b.
b.
(1)必要性:∵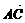 ⊥
⊥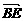 ,∴(b-a)·(a+
,∴(b-a)·(a+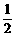 b)=0,
b)=0,
即a·b+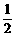 b2-a2-
b2-a2-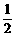 a·b=0.
a·b=0.
∵a⊥b,∴a·b=0.
∴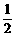 b2-a2=0,即
b2-a2=0,即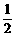 b2=a2,得b2=2a2,|b|=
b2=a2,得b2=2a2,|b|=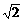 |a|.
|a|.
∴AB∶BC=1∶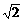 .
.
(2)充分性:∵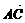 ·
·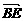 =(b-a)·(a-
=(b-a)·(a-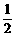 b)=a·b+
b)=a·b+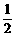 b2-a2-
b2-a2-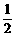 a·b,
a·b,
又∵a⊥b,∴a·b=0.
∴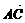 ·
·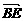 =
=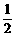 b2-a2=
b2-a2=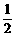 |b|2-|a|2.
|b|2-|a|2.
∵AB∶BC=1∶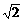 ,∴|a|∶|b|=1∶
,∴|a|∶|b|=1∶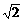 .
.
∴|a|2=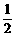 |b|2.∴
|b|2.∴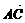 ·
·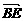 =0.
=0.
故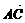 ⊥
⊥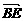 .
.
同理可证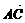 ·
·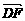 =0,则
=0,则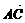 ⊥
⊥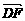 .
.
综合(1)(2)知AC⊥BE,AC⊥DF的充要条件是AB∶BC=1∶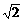 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com