
题目列表(包括答案和解析)
7.如下图,正方体的棱长为3 cm,在每一个面的正中有一个正方形孔通到对面,孔的边长为1 cm,孔的各棱平行于正方体的各棱,则该几何体的总表面积为
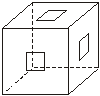
A.54 cm2 B.72 cm2 C.76 cm2 D.84 cm2
解析: 把棱长为3 cm的正方体分割成棱长为1 cm的正方体共有33=27个,如题意抽去三个方向上的正方体,余下的可分为两类.
第一类:处于正方体8个顶点上的8个小正方体,它们算入表面积的面各3个,共3×8=24(cm2);第二类:处于正方体各棱中间的正方体,每个正方体算入表面积的面各4个,共4×12=48(cm2),则总表面积为24+48=72(cm2).
注:此题另一种思路是:外表面积8×6=48(cm2),内表面积2×12=24(cm2),总表面积
72 cm2.
答案: B
6.函数y=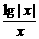 的大致图象是
的大致图象是
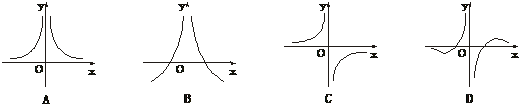
解析: y=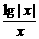 是奇函数,且当x=±1时,y=0,所以选D.
是奇函数,且当x=±1时,y=0,所以选D.
答案: D
5.已知数列an=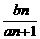 ,其中a>0,b<0(a、b为常数),那么an与an+1的大小关系是
,其中a>0,b<0(a、b为常数),那么an与an+1的大小关系是
A.an>an+1 B.an<an+1 C.an=an+1 D.与n的值相关
解析: 构造函数:an=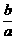 (1-
(1-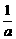 ·
·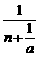 ),
),
由a>0,b<0知an是关于n的减函数,
∴an>an+1.
答案: A
4.已知4a-2b=(-2,2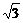 ),c=(1,
),c=(1,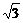 ),a·c=3,|b|=4,则b与c的夹角是
),a·c=3,|b|=4,则b与c的夹角是
A.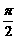 B.
B.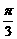 C.
C.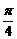 D.
D.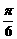
解析: 由题设得4a·c-2b·c=4·3-2b·c=(-2,2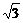 )·(1,
)·(1, 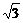 ),
),
故得b·c=4.
所以cosθ=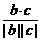 =
=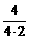 =
= 
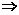 θ=
θ=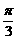 ,
,
故选B
本题主要考查向量数量积的坐标运算及向量数量积公式的灵活应用.
答案:B
3.使得点A(cos2α,sin2α)到点B(cosα,sinα)的距离为1的α的一个值是
A.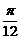 B.
B.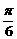 C.-
C.-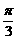 D.-
D.-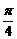
解析: |AB|=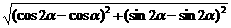 =2|sin
=2|sin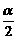 |=1.
|=1.
答案: C
2.用6种不同的颜色把下图中A、B、C、D四块区域分开,允许同一色涂不同的区域,但相邻的区域不能涂同一色,则不同的涂法共有
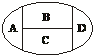
A.400种 B.460种 C.480种 D.496种
解析: 由A→B→C→D的顺序填涂可得,共有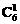 、
、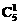 、
、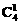 、
、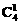 =480种填涂方法.
=480种填涂方法.
答案: C
1.已知集合A={圆:x2+y2=1},B={直线:y=x},则A∩B为
A.{(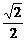 ,
,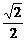 )} B.{(-
)} B.{(-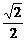 ,-
,-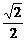 )}
)}
C.{( 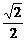 ,
,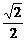 ),(-
),(-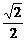 ,
,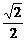 )} D.
)} D.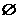
解析: 注意集合中的元素,A为圆,B为直线,故A∩B=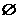 .
.
答案: D
22.(本题满分14分)
(文)已知函数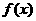 对任意实数
对任意实数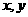 恒有
恒有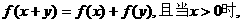
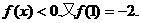
(1)判断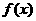 的奇偶性;
的奇偶性;
(2)求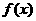 在区间[-3,3]上的最大值;
在区间[-3,3]上的最大值;
(3)解关于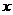 的不等式
的不等式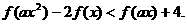
解(1)取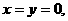 则
则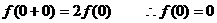 ………………1
………………1
取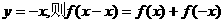
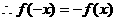 对任意
对任意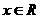 恒成立 ∴
恒成立 ∴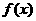 为奇函数. ………………3′
为奇函数. ………………3′
(2)任取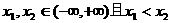 , 则
, 则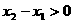
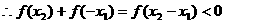 ………………4′
………………4′
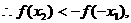 又
又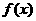 为奇函数
为奇函数 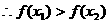
∴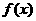 在(-∞,+∞)上是减函数.
在(-∞,+∞)上是减函数.
 对任意
对任意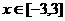 ,恒有
,恒有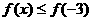 ………………6′
………………6′
而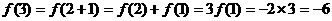
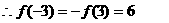
∴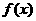 在[-3,3]上的最大值为6………………8′
在[-3,3]上的最大值为6………………8′
(3)∵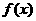 为奇函数,∴整理原式得
为奇函数,∴整理原式得 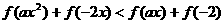
进一步可得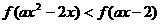
而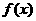 在(-∞,+∞)上是减函数,
在(-∞,+∞)上是减函数,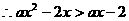 ………………10′
………………10′
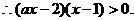
 当
当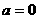 时,
时,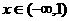
当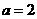 时,
时,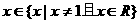 ………………12′
………………12′
当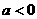 时,
时,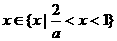 当
当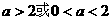 时
时
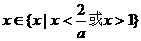 ………………
………………
(理)(本小题满分14分)已知数列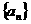 中,
中,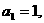 且点
且点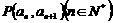 在直线
在直线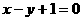 上.
上.
(1)求数列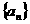 的通项公式;
的通项公式;
(2)若函数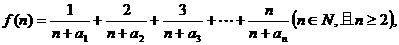 求函数
求函数
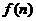 的最小值;
的最小值;
(3)设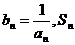 表示数列
表示数列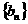 的前项和。试问:是否存在关于
的前项和。试问:是否存在关于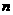 的整式
的整式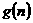 ,使得
,使得
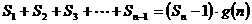 对于一切不小于2的自然数
对于一切不小于2的自然数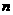 恒成立?若
恒成立?若
存在,写出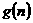 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。


21、假设你正在某公司打工,根据表现,老板给你两个加薪的方案:
(Ⅰ)每年年末加1000元; (Ⅱ)每半年结束时加300元。请你选择。
(1)如果在该公司干10年,问两种方案各加薪多少元?
(2)对于你而言,你会选择其中的哪一种?
解:设方案一第n年年末加薪an,因为每年末加薪1000元,则an=1000n;
设方案二第n个半年加薪bn,因为每半年加薪300元,则bn=300n;
(1)在该公司干10年(20个半年),方案1共加薪S10=a1+a2+……+a10=55000元。
方案2共加薪T20=b1+b2+……+b20=20×300+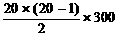 =63000元;……6分
=63000元;……6分
(2)设在该公司干n年,两种方案共加薪分别为:
Sn=a1+a2+……+an=1000×n+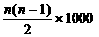 =500n2+500n
=500n2+500n
T2n=b1+b2+……+b2n=2n×300+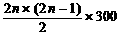 =600n2+300n …………10分
=600n2+300n …………10分
令T2n≥Sn即:600n2+300n>500n2+500n,解得:n≥2,当n=2时等号成立。
∴如果干3年以上(包括3年)应选择第二方案;如果只干2年,随便选;如果只干1年,当然选择第一方案。
20、已知函数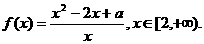
(1)当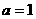 时,求
时,求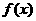 的最小值;
的最小值;
(2)若对任意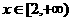 ,
,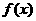
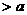 恒成立,求实数
恒成立,求实数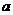 的取值范围.
的取值范围.
解:(1)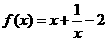 利用定义或导数证明函数的单调性,直接求给与3分
利用定义或导数证明函数的单调性,直接求给与3分
方法解:(1)当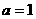 时.
时. 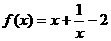
任取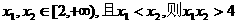 …………2′
…………2′
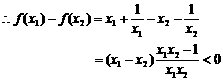
 上是增函数…………4′
上是增函数…………4′
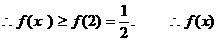 的最小值为
的最小值为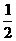 ………………6′
………………6′
(2)依题得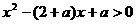 对任意
对任意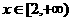 恒成立………………8′
恒成立………………8′
设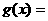
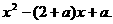 则
则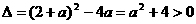
故由二次函数性质可知: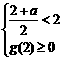 即
即 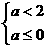 ………………10′
………………10′
解得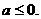 故
故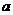 的取值范围是
的取值范围是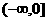 ………………12′
………………12′
解法2:依题可得方程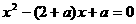 其判别式
其判别式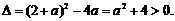
 设方程两根为
设方程两根为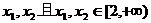
则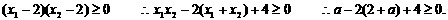
解得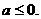 ∴
∴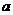 的取值范围是
的取值范围是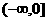
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com