
题目列表(包括答案和解析)
2.设向量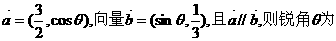 ( )
( )
A.60° B.30° C.75° D.45°
有一项是符合题目要求的.)
1.设p、q是两个命题,则“复合命题p或q为真,p且q为假”的充要条件是 ( )
A.p、q中至少有一个为真 B.p、q中至少有一个为假
C.p、q中有且只有一个为真 D.p为真,q为假
11. 由原点O向三次曲线y=x3-3ax2+b x (a≠0)引切线,切于不同于点O的点P1(x1,y1),再由P1引此曲线的切线,切于不同于P1的点P2(x2,y2),如此继续地作下去,……,得到点列{ P n(x n , y n)},试回答下列问题:
(1) 求x1;
(2) 求x n与x n+1的关系;
(3) 若a>0,求证:当n为正偶数时, x n<a;当n为正奇数时, x n>a.
解答:(1)由y=x3-3ax2+b x, ①
得y′=3x2-6ax+b.
过曲线①上点P1(x1, y1)的切线l1的方程是
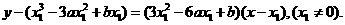
由它过原点,有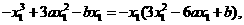
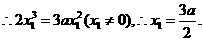
(2)过曲线①上点Pn+1(xn+1,yn+1)的切线ln+1的方程是
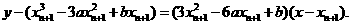
由ln+1过曲线①上点P n(x n, yn),有
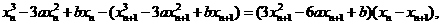
∵x n-xn+1≠0,以x n-xn+1除上式,得
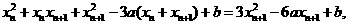
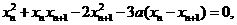 以x n-xn+1除之,得x n+2xn+1-3a=0.
以x n-xn+1除之,得x n+2xn+1-3a=0.
(3) 由(2)得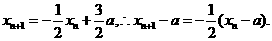
故数列{x n-a}是以x 1-a=为首项,公比为-的等比数列,
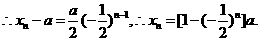
∵a>0,∴当n为正偶数时, 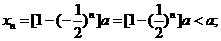
当n为正奇数时, 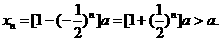
10.
设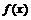 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,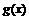 的图象与
的图象与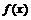 的图象关于直线
的图象关于直线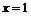 对称,且当
对称,且当
x∈[ 2,3 ] 时,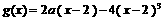 222233.
222233.
(1)求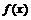 的解析式;
的解析式;
(2)若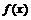 在
在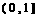 上为增函数,求
上为增函数,求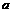 的取值范围;
的取值范围;
(3)是否存在正整数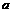 ,使
,使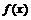 的图象的最高点落在直线
的图象的最高点落在直线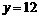 上?若存在,求出
上?若存在,求出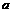 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解答: (1)当x∈[-1,0]时,2-x∈[2,3],f(x)=g(2-x)= -2ax+4x3;当x∈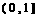 时,f(x)=f(-x)=2ax-4x3,
时,f(x)=f(-x)=2ax-4x3,
∴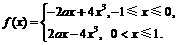 …………………………………………………4分
…………………………………………………4分
(2)由题设知,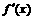 >0对x∈
>0对x∈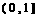 恒成立,即2a-12x2>0对x∈
恒成立,即2a-12x2>0对x∈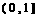 恒成立,于是,a>6x2,从而a>(6x2)max=6.…………………………………………………8分
恒成立,于是,a>6x2,从而a>(6x2)max=6.…………………………………………………8分
(3)因f(x)为偶函数,故只需研究函数f(x)=2ax-4x3在x∈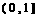 的最大值.
的最大值.
令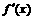 =2a-12x2=0,得
=2a-12x2=0,得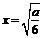 .…………10分 若
.…………10分 若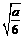 ∈
∈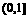 ,即0<a≤6,则
,即0<a≤6,则
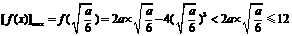 ,
,
故此时不存在符合题意的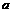 ;
;
若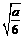 >1,即a>6,则
>1,即a>6,则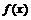 在
在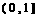 上为增函数,于是
上为增函数,于是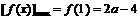 .
.
令2a-4=12,故a=8. 综上,存在a = 8满足题设.…………………………14分
9.
已知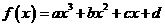 是定义在R上的函数,其图象交
是定义在R上的函数,其图象交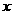 轴于A、B、C两点,若B点坐标为
轴于A、B、C两点,若B点坐标为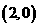 ,且
,且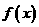 在
在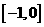 和
和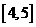 上有相同的单调性,在
上有相同的单调性,在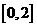 和
和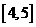 上有相反的单调性。
上有相反的单调性。
(1)求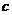 的值;
的值;
(2)在函数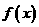 的图象上是否存在一点
的图象上是否存在一点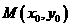 ,使得
,使得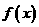 在点M的切线的斜率为
在点M的切线的斜率为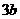 ?若存在,求出M点的坐标;若不存在,说明理由。
?若存在,求出M点的坐标;若不存在,说明理由。
(3)求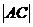 的取值范围。
的取值范围。
解答:(1)因为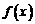 在
在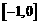 和
和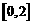 上有相反的单调性
上有相反的单调性
所以 的一个极值点,故
的一个极值点,故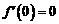
即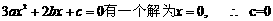 …………………………2分
…………………………2分
(2)因为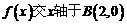
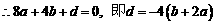
令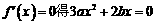
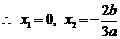
因为在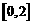 和
和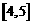 上有相反的单调性
上有相反的单调性
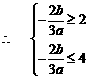
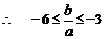 ………………………………………………………………5分
………………………………………………………………5分
假设存在点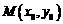 使得
使得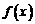 在点M的切线的斜率为
在点M的切线的斜率为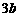
则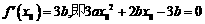
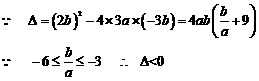
故不存在点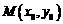 满足(2)中的条件。……………………………………8分
满足(2)中的条件。……………………………………8分
(3)设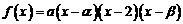
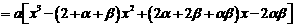
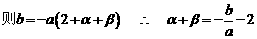
 ………………………………………10分
………………………………………10分
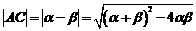
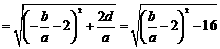 …………………………………………12分
…………………………………………12分
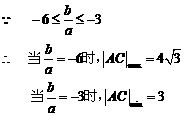
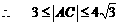 ……………………………………………………………14分
……………………………………………………………14分
8.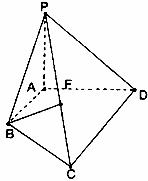 如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=
如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=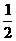 CD.
CD.
(1)点F在线段PC上运动,且设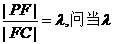 为何值时,BF//平面PAD?并证明你的结论;
为何值时,BF//平面PAD?并证明你的结论;
(2)二面角F-CD-B为45°,求二面角B-PC-D的大小;
(3)在(Ⅱ)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
解答:(1)当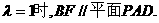 (1分)
(1分)
证明:取PD中点E,则EF//CD,且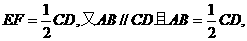
∴四边形ABFE为平行四边形. (3分)
∴BF//AE. 又AE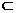 平面PAD ∴BF//平面PAD (4分)
平面PAD ∴BF//平面PAD (4分)
(2)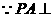 平面ABCD,
平面ABCD,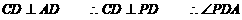 即是二面角的平
即是二面角的平
面角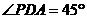 (5分)
(5分)
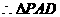 为等腰直角三角形,
为等腰直角三角形,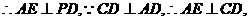
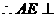 平面PCD 又BF//AE,
平面PCD 又BF//AE,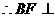 平面PCD.
平面PCD. 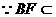 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B-PC-D的大小为90°. (8分)
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD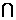
平面PBC=PC知:EH⊥平面PBC. (9分)
在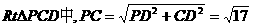 ,
,
在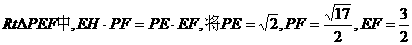 代入得:
代入得:
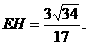 即点E到平面PBC的距离为
即点E到平面PBC的距离为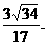 (11分)
(11分)
又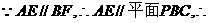 点A到平面PBC的距离为
点A到平面PBC的距离为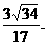 (12分)
(12分)
7.
有一批产品出厂前要进行五项指标检验,如果有两项指标不合格,则这批食品不能出厂,已知每项指标抽检是相互独立的,每项指标抽检出现不合格品的概率都是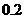 。
。
(1)求这批产品不能出厂的概率(保留三位有效数学)
(2)求直至五项指标全部检验完毕,才能确定该批产品是否出厂的概率(保留三位有效数学)
解答: (1)这批产品不能出厂的概率是: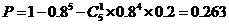
五项指标全部检验完毕,这批食品可以出厂的概率是: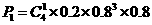
五项指标全部检验完毕,这批食品不能出厂的概率是: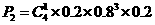
由互斥事件有一个发生的概率加法可知:五项指标全部检验完毕才能确定这批产品是否可以出厂的概率是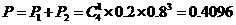
6.
已知函数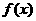 =
=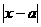 ,
,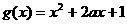 (a为正常数),且函数
(a为正常数),且函数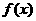 与
与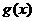 的图象在y轴上的截距相等.
的图象在y轴上的截距相等.
(1)求a的值;
(2)求函数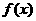 -
-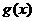 的单调递增区间.
的单调递增区间.
解答:(1)由题意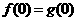 ,
, =1又a>0,所以a=1.
=1又a>0,所以a=1.
(2)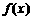
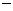 g(x)=
g(x)=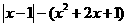 ,当
,当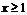 时,
时,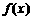
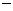
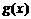 =
=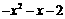 ,无递增区间;当x<1时,
,无递增区间;当x<1时,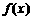
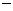
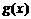 =
=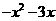 ,它的递增区间是
,它的递增区间是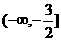 .
.
综上知: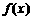
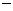
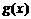 的单调递增区间是
的单调递增区间是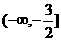 .
.
5.函数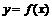 的图象如图所示,则导函数
的图象如图所示,则导函数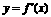 的图象大致是 (D)
的图象大致是 (D)
4.已知函数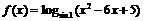 在
在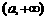 上是减函数,则实数a的取值范围为 (D)
上是减函数,则实数a的取值范围为 (D)
A. (5,+∞) B.
(3,+∞) C. (-∞,3) D. 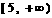
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com