
题目列表(包括答案和解析)
13.若球的大圆面积为3π,则该球的体积为 .
12.设奇函数f (x )在[-1,1]上是增函数,且f (-1)= 一1.若函数,,f (x ) ≤ t 2一2 a t +l对所有的 x∈[一1.1]都成立,则当a∈[1,1]时,t 的取值范围是 ( )
(A)一2≤t≤2 (B)
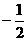 ≤t≤
≤t≤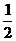
(C) t≥2或t≤一2或t = 0
(D) t≥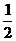 或t≤
或t≤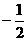 或t=0。
或t=0。
11. a, b是异面直线,A、B∈a, C、D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a与b所成的角为 ( )
A.30° B.60° C.90° D.45°
8.已知x , y∈Z.则满足 x+y≤5 的点(x ,y)的个数为 ( )
y≥o
(A) 9 (B)10 (C) 11 (D)12
9已知函数,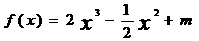 (m为常数)图像上点A处的切线与直线2一y+3=0的夹角为45o。则点A的横坐标为
( )
(m为常数)图像上点A处的切线与直线2一y+3=0的夹角为45o。则点A的横坐标为
( )
(A) 0 (B) 1 (C) 0或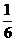 (D) l或
(D) l或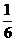
1O.设双曲线16x2-9y 22 = 144的右焦点为F2,M是双曲线上任意一点 , 点A的坐标为
(9,2).则 |MA|+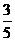 |MF2| 的最小值为 ( )
|MF2| 的最小值为 ( )
(A) 9
(B) 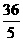 (C)
(C)
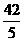 (D)
(D) 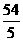
2.不等式|x|(1-3x)>0的解集是 ( )
A.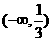 B.
B.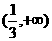 C.
C. 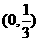 D.
D.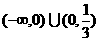
3函数y=2x+1(-1≤x<0)的反函数是 ( )
A.y=1+log2x(x>0) B.y=-1+log2x(x>0)C.y=1+log2x(1≤x<2)D.y=-1+log2x(1≤x<2)
4设向量确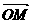 = (3,一3),
= (3,一3),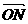 = (一5,一1),则
= (一5,一1),则 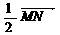 等于 ( )
等于 ( )
(A)(一2, 4) (B)(-1,一2) (C)(4.一1) (D)(一4,1)
5设等比数列{an}的首项为a1,公比为q,则“a1<O,且0<q<1”是“对于任意正整数n,都有 an+1>an”的 ( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
6设l1 、l2为两条直线,a、β为两个平面,给出下列四个命题:
(1)若l1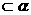 , l2
, l2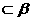 ,l1∥β,l1∥a则a∥β. (2)若l1⊥a ,l2⊥a,则l1∥l2
,l1∥β,l1∥a则a∥β. (2)若l1⊥a ,l2⊥a,则l1∥l2
(3)若l1∥a,l1∥l2,则l2∥a (4)若a⊥β,l1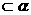 ,,则l1⊥β
,,则l1⊥β
其中,正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
7设函数,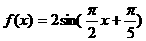 若对任意x∈R,都有,f (x1 )≤f (x )≤f (x2 )成立,则|x1 -x2|的最小值为
( )
若对任意x∈R,都有,f (x1 )≤f (x )≤f (x2 )成立,则|x1 -x2|的最小值为
( )
(A)4 (B)2
(C)1 (D) 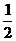
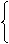 x-y≥O
x-y≥O
1.不等式 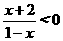 的解集为
( )
的解集为
( )
(A)(一2.1) (B)(一1,2) (C)(一∞,一2) ∪(1,+∞) (D)(一∞,一1)∪(2,+∞)
22.(14分)设数列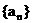 的各项都是正数, 且对任意
的各项都是正数, 且对任意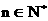 都有
都有
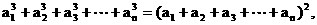 记
记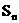 为数列
为数列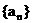 的前n项和.
的前n项和.
(1) 求证: 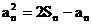 ;
;
(2) 求数列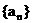 的通项公式;
的通项公式;
(3) 若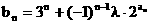 (
(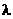 为非零常数,
为非零常数, 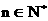 ), 问是否存在整数
), 问是否存在整数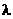 , 使得对任意
, 使得对任意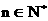 , 都有
, 都有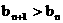 .
.
21.(12分)已知椭圆E的右焦点F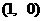 , 右准线l:
, 右准线l: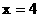 , 离心率
, 离心率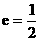 .
.
(1) 求椭圆E的方程;
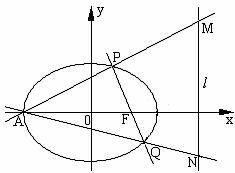
(2) 设A是椭圆E的左顶点, 一经过右焦点F的直线与椭圆E相交于P、Q两点(P、Q与A不重合), 直线AP、AQ分别与右准线l相交于点M、N, 求证: 直线PN、直线QM与x轴相交于同一点.
20.(12分)已知函数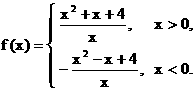
(1) 求证: 函数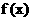 是偶函数;
是偶函数;
(2) 判断函数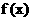 分别在区间
分别在区间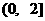 、
、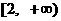 上的单调性, 并加以证明;
上的单调性, 并加以证明;
(3) 若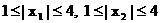 , 求证:
, 求证: 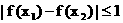 .
.
19.(12分)设某银行一年内吸纳储户存款的总数与银行付给储户年利率的平方成正比, 若
该银行在吸纳到储户存款后即以5%的年利率把储户存款总数的90%贷出以获取利润, 问银行支付给储户年利率定为多少时, 才能获得最大利润?
(注: 银行获得的年利润是贷出款额的年利息与支付给储户的年利息之差.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com