
题目列表(包括答案和解析)
22、已知定点R的坐标为(0,-3),点P在x轴上,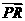 ⊥
⊥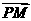 ,线段PM与y轴交于点Q,且满足
,线段PM与y轴交于点Q,且满足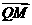 =2
=2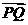
(1) 若点P在x轴上运动,求点M的轨迹E;
(2) 求轨迹E的倾斜角为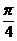 的切线
的切线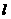 0的方程;
0的方程;
(3) 若(2)中切线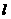 0与y轴交于点G,过G的直线
0与y轴交于点G,过G的直线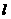 与轨迹E交于A、B两点,点D的坐标为 (0,1),当∠ADB为钝角时,求直线
与轨迹E交于A、B两点,点D的坐标为 (0,1),当∠ADB为钝角时,求直线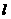 的斜率的取值范围。
的斜率的取值范围。
21、已知数列{an}的前n项和为Sn,又有数列{bn},它们满足关系b1=a1,对n∈N+,有an=n-Sn , bn+1=an+1-an.
(1)求{bn}通项公式
(2)求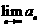
(3)若令Cn= 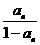 ,求满足C1+C2+…+Cn<400的最大的正整数n.
,求满足C1+C2+…+Cn<400的最大的正整数n.
20..、已知函数f(x)=ax2+bx+1(a,b∈R)
(1)若 f(-1)=0,且对任意实数x均有f(x) ≥0成立,求f(x)表达式
(2)在(1)条件下,当x∈[-2,2]时,S(x)=xf(x)-kx单调递增,求实数k取值范围.
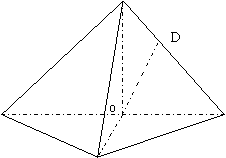
19、如图:在三棱锥P-ABC中,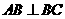
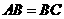 =m,点O、D分别为AC、PC中点,OP上底面ABC
=m,点O、D分别为AC、PC中点,OP上底面ABC
(1)求证: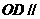 平面PAB
平面PAB
(2)当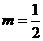 时,求直线PA与平面PBC所成角的大小
时,求直线PA与平面PBC所成角的大小
(3)当m取何值时,O在平面PBC内的射影恰好为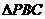 的重心。
的重心。
|
|
|
|

17 已知
已知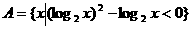 ,
, ,且
,且 ,求实数
,求实数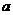 的取值范围
的取值范围
18、已知点 A(2,0),B(0,2),C(cos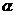 ,sin
,sin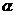 ),且0<
),且0<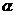 <
<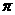
(I) 若|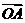 +
+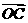 |=
|=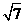 ,求
,求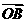 与
与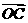 的夹角;
的夹角;
(II)若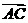 ⊥
⊥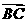 ,求tan
,求tan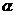 的值。
的值。
16、直线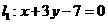 ,
,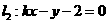 与
与 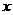 轴,
轴,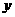 轴的正半轴围成的四边形有外接圆,则k=
轴的正半轴围成的四边形有外接圆,则k=
15.已知A (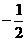 ,0 ),B是圆
,0 ),B是圆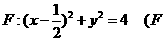 为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为
.
14、设实数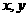 满足约束条件
满足约束条件 则
则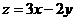 的最大值
的最大值
13、已知向量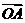 =(k,12),
=(k,12),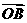 =(4,5),
=(4,5),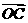 =(-k,10),且A、B、C三点共线,则k=______.
=(-k,10),且A、B、C三点共线,则k=______.
12、下面四个命题:
①
“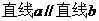 ”的充要条件是“
”的充要条件是“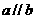 所在“平面””
所在“平面””
②
“直线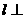 平面
平面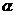 内所有直线”的充要条件是“
内所有直线”的充要条件是“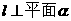 ”
”
③ “直线a、b为异面直线”的充分不必要条件是“a、b不相交”
④ “平面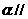 平面
平面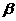 ”的必要不充分条件是“平面
”的必要不充分条件是“平面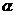 内存在不等线三点到平面
内存在不等线三点到平面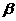 的距离相等”
的距离相等”
其中正确命题的序号是:( )
A、①② B、②③ C、③④ D、②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com