
题目列表(包括答案和解析)
17.解: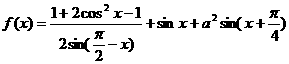
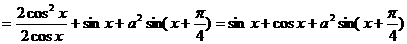
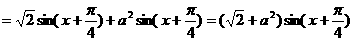
因为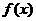 的最大值为
的最大值为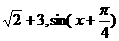 的最大值为1,则
的最大值为1,则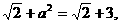
所以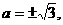 17.(福建卷)
17.(福建卷)
已知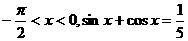 .
.
(I)求sinx-cosx的值;
(Ⅱ)求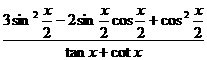 的值.
的值.
17.(重庆卷)若函数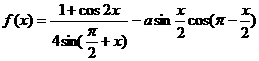 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
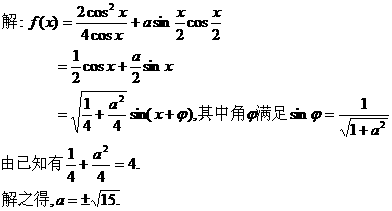 17.(重庆卷)
17.(重庆卷)
若函数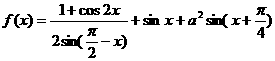 的最大值为
的最大值为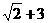 ,试确定常数a的值.
,试确定常数a的值.
16.解法一 由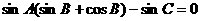 得
得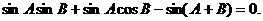
所以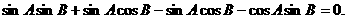 即
即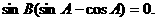
因为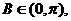 所以
所以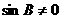 ,从而
,从而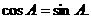
由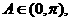 知
知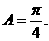 从而
从而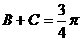 .
.
由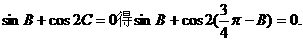
即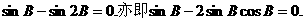
由此得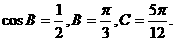 所以
所以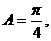
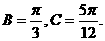
解法二:由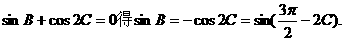
由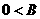 、
、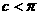 ,所以
,所以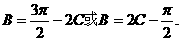 即
即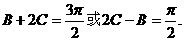
由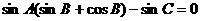 得
得 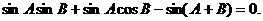
所以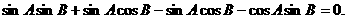
即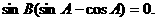 因为
因为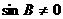 ,所以
,所以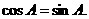
由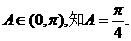 从而
从而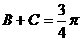 ,知B+2C=
,知B+2C=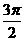 不合要求.
不合要求.
再由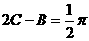 ,得
,得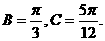 所以
所以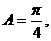
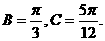
16.(湖南卷)
已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
18.解: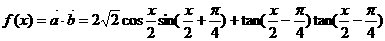
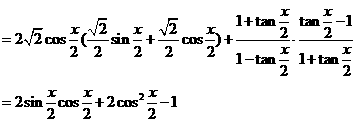
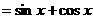
=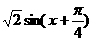 .
.
所以 ,最小正周期为
,最小正周期为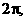
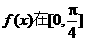 上单调增加,
上单调增加,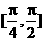 上单调减少.
上单调减少.
18.(江西卷)
已知向量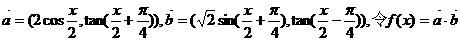 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
15.(浙江卷)已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ) 求f(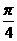 )的值;(Ⅱ) 设
)的值;(Ⅱ) 设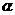 ∈(0,
∈(0,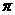 ),f(
),f( )=
)=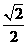 ,求sin
,求sin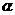 的值.
的值.
解:(Ⅰ)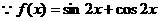
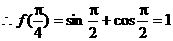
(Ⅱ) 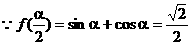
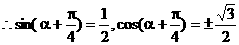
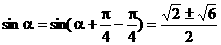
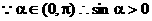
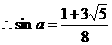
15.(浙江卷)已知函数f(x)=-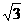 sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f(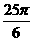 )的值; (Ⅱ) 设
)的值; (Ⅱ) 设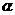 ∈(0,
∈(0,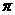 ),f(
),f( )=
)=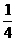 -
-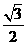 ,求sin
,求sin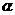 的值.
的值.
解:(Ⅰ) 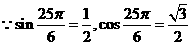
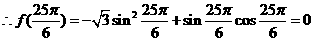
(Ⅱ) 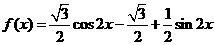
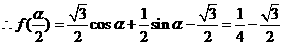
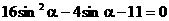 解得
解得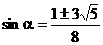
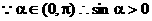
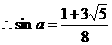
17.本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分.
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,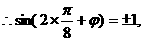
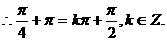
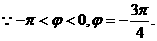
(Ⅱ)由(Ⅰ)知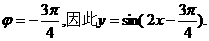
由题意得 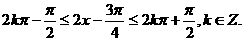
所以函数
(Ⅲ)由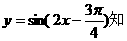
|
x |
0 |
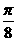 |
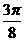 |
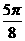 |
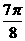 |
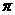 |
|
y |
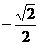 |
-1 |
0 |
1 |
0 |
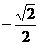 |
 故函数
故函数
(17)(全国卷Ⅱ)已知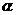 为第二象限的角,
为第二象限的角,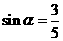 ,
,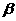 为第一象限的角,
为第一象限的角,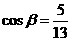 .求
.求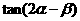 的值.
的值.
(17) (全国卷Ⅲ)
已知函数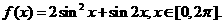 求使
求使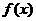 为正值的
为正值的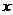 的集合.
的集合.
解:∵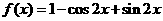 ………………………………………………2分
………………………………………………2分
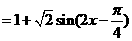 …………………………………………………4分
…………………………………………………4分
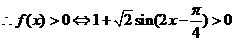
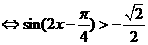 …………6分
…………6分
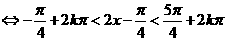 …………………………8分
…………………………8分
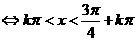 …………………………………………10分
…………………………………………10分
又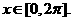 ∴
∴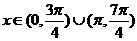 ………………………12分
………………………12分
15.解:
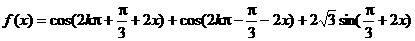
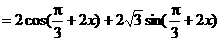

所以函数f(x)的值域为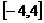 ,最小正周期
,最小正周期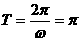
(15)(北京卷) 已知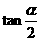 =2,求
=2,求
(I)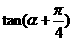 的值; (II)
的值; (II)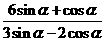 的值.
的值.
解:(I)∵
tan =2, ∴
=2, ∴ 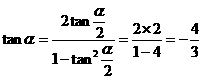 ;
;
所以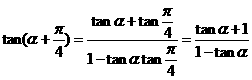 =
=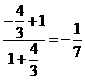 ;
;
(II)由(I), tanα=-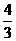 , 所以
, 所以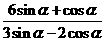 =
=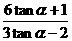 =
=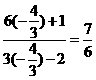 .
.
(15)(北京卷) 已知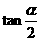 =2,求
=2,求
(I)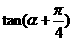 的值; (II)
的值; (II)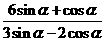 的值.
的值.
解:(I)∵
tan =2, ∴
=2, ∴ 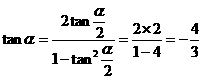 ;
;
所以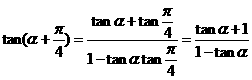 =
=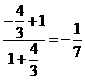 ;
;
(II)由(I), tanα=-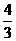 , 所以
, 所以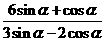 =
=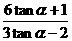 =
=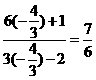 .
.
(17)(全国卷Ⅰ)
设函数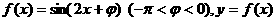 图像的一条对称轴是直线
图像的一条对称轴是直线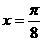 。
。
(Ⅰ)求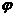 ;(Ⅱ)求函数
;(Ⅱ)求函数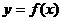 的单调增区间;
的单调增区间;
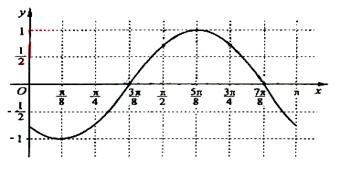
(Ⅲ)画出函数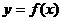 在区间
在区间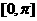 上的图像。
上的图像。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com