
题目列表(包括答案和解析)
3.在数列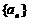 中,a1=2,
中,a1=2, 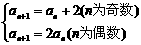 ,则a5等于
,则a5等于
A.12 B.14 C.20 D.22
2.数列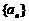 满足
满足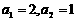 并且
并且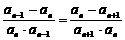 (
(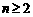 )。则数列的第100项为
)。则数列的第100项为
A.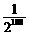 B.
B.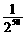 C.
C.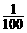 D.
D.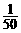
1.把数列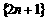 依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)…则第104个括号内各数之和为
依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)…则第104个括号内各数之和为
A.2036 B.2048 C.2060 D.2072
22、解:(Ⅰ).令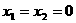 ,依条件(3)可得f (0+0)≥f (0)+f (0),即f (0)
,依条件(3)可得f (0+0)≥f (0)+f (0),即f (0) ≤0
≤0
又由条件(1)得f (0) ≥0,则f (0)= 0
(Ⅱ)任取0≤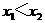 ≤1,可知
≤1,可知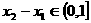 ,
,
则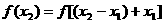

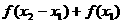 ,
,
即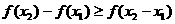 ≥0,故
≥0,故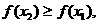 于是当0≤x≤1时,有f (x) ≤f (1)
=1,因此,当x=1时,f (x)有最大值1
于是当0≤x≤1时,有f (x) ≤f (1)
=1,因此,当x=1时,f (x)有最大值1
(Ⅲ)证明:当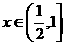 时,f (x) ≤1<2x
时,f (x) ≤1<2x
当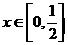 时,f (2x) ≥f (x)+f
(x)=2f
(x),∴
时,f (2x) ≥f (x)+f
(x)=2f
(x),∴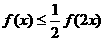
(Ⅳ)证明:当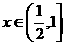 时,f (x) ≤1≤2x
时,f (x) ≤1≤2x
当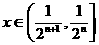 时,f (2x) ≥f (x)+f
(x)=2 f(x),∴
时,f (2x) ≥f (x)+f
(x)=2 f(x),∴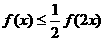 ,
,
显然,当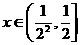 时,
时,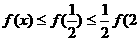 ·
·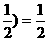 ·
·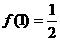 成立
成立
假设当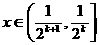 时,有
时,有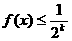 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当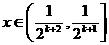 时,
时,
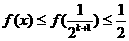 ·
·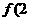 ·
·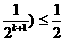 ·
·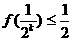 ·
·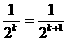
可知对于 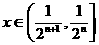 ,总有
,总有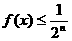 ,其中n∈N*
,其中n∈N*
此时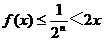 ,故
,故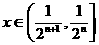 时,有f (x)<2x (n∈N*)
时,有f (x)<2x (n∈N*)
21、解:⑴令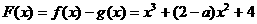
∴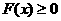 在
在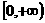 上恒成立,等价于
上恒成立,等价于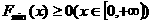
若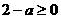 ,显然
,显然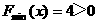
若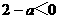 ,
,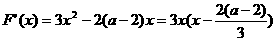
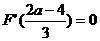 且当
且当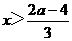 时,
时,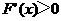 ;当
;当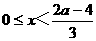 时,
时,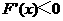
∴ 当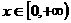 ,
, 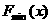 =
=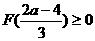
即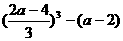 ·
·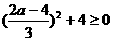 解得 a≤5 ∴2<a≤5
解得 a≤5 ∴2<a≤5
∴ a的范围是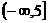
⑵由题意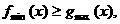
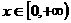
显然 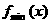 =
=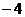 (当x=0时,取最小值)
(当x=0时,取最小值)
 a≥0时,g(x)无最大值, 不合题意,∴a<0.
a≥0时,g(x)无最大值, 不合题意,∴a<0.
又
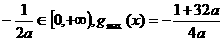 ,
,
∴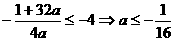 ,
,
∴a的范围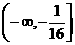 .
.
20、解:⑴ 不等式
不等式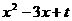 <0的解集为
<0的解集为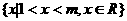 ∴
∴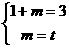 得
得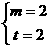
⑵ f(x)=
f(x)=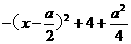 在
在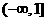 上递增,∴
上递增,∴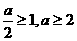
又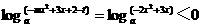 ,
,
由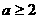 ,可知0<
,可知0<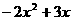 <1
<1
由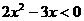 , 得0<x<
, 得0<x<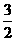
由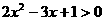 得x<
得x<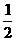 或x>1
或x>1
故原不等式的解集为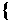 x|0<x<
x|0<x<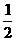 或1<x<
或1<x<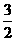
19、解:原不等式化为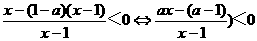 …………(*)
…………(*)
⑴当 a>0时,(*)等价于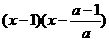 <0
<0
 a>0时,
a>0时,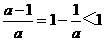
∴不等式的解为: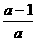 <x<1
<x<1
⑵当a=0时,(*)等价于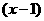 <0即x<1
<0即x<1
⑶当a<0时,(*)等价于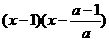 >0
>0
 a<0时,
a<0时,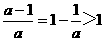
∴ 不等式的解为 : x<1或x>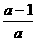
综上所述:当a>0时,不等式的解集为(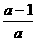 ,1);当a=0时,不等式的解集为
,1);当a=0时,不等式的解集为 ;
;
当a<0时,不等式的解集为 ∪(
∪(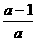 ,
, )
)
18、解:原不等式等价于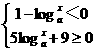 ……..(1)或
……..(1)或 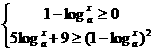 ………..(2)
………..(2)
由(1)得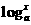 >1
由(2)得
>1
由(2)得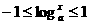
由(1)(2)得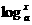
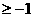
当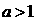 时,原不等式的解集为
时,原不等式的解集为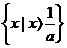 ;当
;当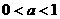 时,原不等式的解集为
时,原不等式的解集为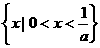
17、解:原不等式等价于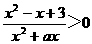
由于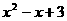 >
> 对x
对x R恒成立 ,∴
R恒成立 ,∴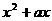 >0即x(x+a)>0 (6分)
>0即x(x+a)>0 (6分)
当a 时,
时,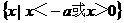 ;当a=0时
;当a=0时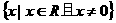 ;当a
;当a 时,
时,
15、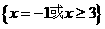 16、
16、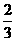
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com