
题目列表(包括答案和解析)
8、已知实数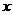 、
、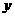 满足
满足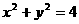 ,则
,则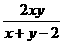 的最小值为 ( )
的最小值为 ( )
A.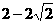 B.
B.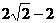 C.
C.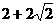 D.
D.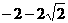
7、已知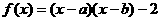 ,并且
,并且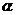 、
、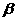 是方程
是方程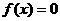 的两根,实数
的两根,实数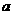 ,
,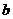 ,
,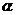 ,
,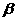 的大小关系可能是 ( )
的大小关系可能是 ( )
A.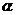 <
<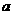 <
<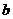 <
<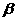 B.
B.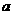 <
<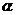 <
<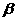 <
<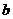
C.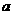 <
<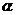 <
<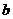 <
<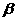 D.
D.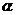 <
<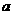 <
<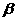 <
<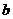
6、已知数列{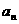 }的通项式是
}的通项式是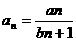 ,其中
,其中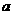 ,
,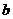 是正常数,那么
是正常数,那么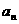 与
与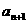 的大小关系为 ( )
的大小关系为 ( )
A.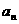 <
<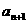 B.
B.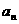 >
>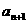 C.
C.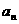 =
=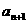 D.与
D.与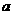 ,
,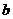 的取值有关
的取值有关
5、△ABC的周长为20,面积为10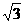 ,A=60º,则BC边的长为 ( )
,A=60º,则BC边的长为 ( )
A.5 B.6 C.7 D.8
4、已知函数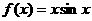 ,则
,则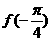 、
、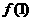 及
及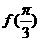 的大小关系为 ( )
的大小关系为 ( )
A.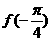 >
>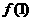 >
>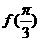 B.
B.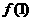 >
>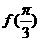 >
>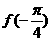
C.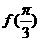 >
>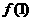 >
>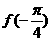 D.
D.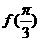 >
>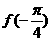 >
>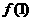
3、等差数列{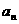 }中,
}中,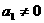 ,
,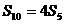 ,则适合
,则适合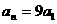 的
的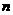 的值为 ( )
的值为 ( )
A.6 B.5 C.4 D.3
2、已知函数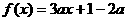 ,在(
,在(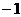 ,1)内存在实数
,1)内存在实数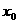 ,使
,使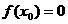 ,则
,则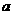 的取值范围是 ( )
的取值范围是 ( )
A.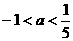 B.
B.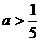 C.
C.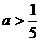 或
或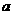 <
<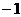 D.
D.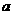 >
>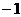
1、若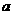 、
、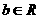 ,则使|
,则使|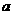 |+|
|+|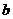 |>1成立的一个充分不必要的条件是 ( )
|>1成立的一个充分不必要的条件是 ( )
A.|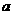 +
+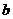 |≥1 B.|
|≥1 B.|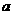 |≥
|≥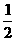 且|
且|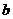 |≥
|≥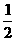 C.
C.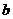 <
<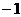 D.
D.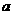 ≥1
≥1
3.培养运用不等式研究函数、方程等问题及运用函数、方程等思想解决不等式问题的能力.
例题讲解
例题1
(1) 关于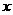 的不等式
的不等式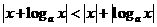 (
(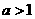 )的解为 ( )
)的解为 ( )
A 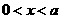 B
B 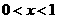 C
C 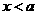 D
D 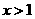
(2) 设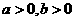 ,则下列不等式不恒成立的是 ( )
,则下列不等式不恒成立的是 ( )
A 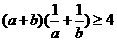 B
B 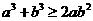
C 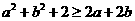 D
D
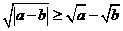
(3) 设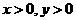 且
且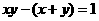 则
( )
则
( )
A 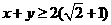 B
B 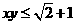
C 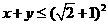 D
D 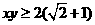
(4)在R上定义运算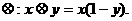 若不等式
若不等式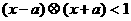 对任意实数
对任意实数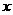 成立,则 ( )
成立,则 ( )
A
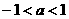 B
B
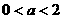 C
C
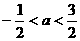 D
D
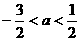
(5) 已知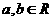 ,
,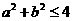 ,则
,则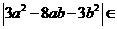 __________.
__________.
(6) 已知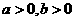 ,则函数
,则函数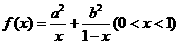 的最小值是_______.
的最小值是_______.
例题2
某村计划建造一个室内面积为800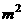 的矩形蔬菜温室。在温室内,沿左、右两侧后
的矩形蔬菜温室。在温室内,沿左、右两侧后
侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
例题3 已知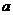 为实数,
为实数,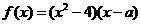
(1)
求导数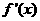 ;
;
(2)
若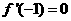 ,求
,求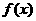 在
在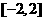 上的最大值和最小值;
上的最大值和最小值;
(3)
若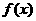 在
在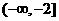 和
和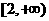 上都是递增的,求
上都是递增的,求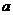 的取值范围.
的取值范围.
例题4 设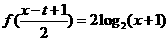
(1) 当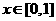 时,
时,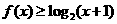 恒成立,求
恒成立,求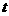 的取值范围;
的取值范围;
(2) 当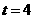 时,
时, 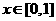 ,求
,求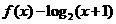 的最小值.
的最小值.
例题5已知实数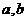 满足:关于
满足:关于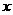 的不等式
的不等式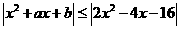 对一切
对一切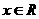 均成立.
均成立.
(1)
请验证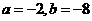 满足题意;
满足题意;
(2)
求出所有满足题意的实数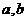 ,并说明理由;
,并说明理由;
(3)
若对一切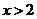 ,均有不等式
,均有不等式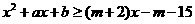 成立,求实数
成立,求实数 的取值范围.
的取值范围.
2.能够利用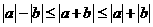 讨论一些问题;
讨论一些问题;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com