
题目列表(包括答案和解析)
4、抛物线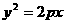 ,横坐标为4的点到焦点的距离为5,则P=___________.
,横坐标为4的点到焦点的距离为5,则P=___________.
3、椭圆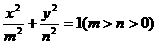 与双曲线
与双曲线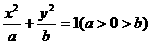 共焦点F1,F2,P是两曲线交点,则|PF1|·|PF2|的值是_________(
共焦点F1,F2,P是两曲线交点,则|PF1|·|PF2|的值是_________(
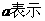 ).
).
2、正三角形的三个顶点在双曲线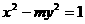 的右支上,其中一个顶点是双曲线的右顶点,则m
的右支上,其中一个顶点是双曲线的右顶点,则m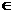 ________.
________.
1、a、b、c分别是双曲线的实半轴,虚半轴和半焦距,若方程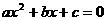 无实根,则离心率
无实根,则离心率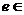 _________.
_________.
4、实数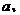
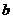 变化时,直线
变化时,直线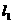 :
: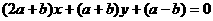 恒过直线
恒过直线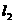 :
: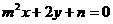 上的一个定点,则点
上的一个定点,则点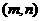 满足的曲线方程是_____________.
满足的曲线方程是_____________.
例题讲解
例1、求证:当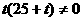 时,方程
时,方程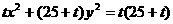 表示的曲线具有相同的焦点.
表示的曲线具有相同的焦点.
例2、椭圆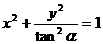
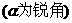 的焦点在
的焦点在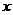 轴上,A是右顶点,椭圆与射线
轴上,A是右顶点,椭圆与射线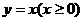 的交点是B,以A为焦点,过点B且开口向左的抛物线顶点为
的交点是B,以A为焦点,过点B且开口向左的抛物线顶点为 ,当椭圆离心率
,当椭圆离心率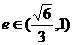 时,求:
时,求: 的范围.
的范围.
例3、函数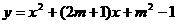 .①
.① 取何值时,
取何值时,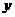 的最小值是0?
的最小值是0?
②求证:不论 是什么值,函数图象的顶点在同一直线上.
是什么值,函数图象的顶点在同一直线上.
③平行于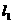 的直线中,哪些与抛物线相交?哪些不与抛物线相交?
的直线中,哪些与抛物线相交?哪些不与抛物线相交?
④求证:任一平行于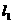 且与抛物线相交的直线,被抛物线截出的线段都相等.
且与抛物线相交的直线,被抛物线截出的线段都相等.
课后作业
班级_______学号__________姓名_________
3、点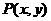 在曲线
在曲线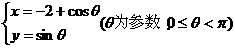 ,则
,则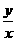 的范围是__________.
的范围是__________.
2、抛物线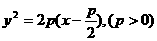 ,与直线
,与直线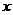 ·
·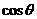 +
+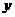 ·
·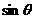 =
=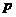 ·
·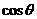 的位置关系是__________.
的位置关系是__________.
1、动点P分别与两个定点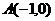 ,
,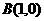 连线的斜率之积等于
连线的斜率之积等于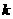 ,则当
,则当 时,动点P在一个圆周上运动;当______________时,P在一个椭圆上运动;当_________时,P在一条双曲线上运动.
时,动点P在一个圆周上运动;当______________时,P在一个椭圆上运动;当_________时,P在一条双曲线上运动.
8、设椭圆 :
: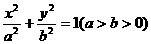 ,曲线
,曲线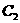 :
: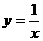 ,且
,且 与
与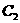 在第一象限内只有一个公共点P.
在第一象限内只有一个公共点P.
(1)试用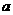 表示
表示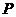 的坐标;
的坐标;
(2)设A、B是椭圆 的两个焦点,当
的两个焦点,当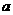 变化时,求△ABP的面积函数
变化时,求△ABP的面积函数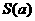 的值域;
的值域;
(3)记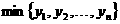 为
为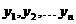 中最小的一个,设
中最小的一个,设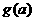 是以椭圆
是以椭圆 的半焦距为边长的正方形的面积,求:
的半焦距为边长的正方形的面积,求: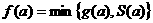 的表达式.
的表达式.
高三数学教学案 第八章 圆锥曲线
第十二课时 含参系数的曲线方程(二)
考纲摘录
根据曲线方程研究它的几何性质.
难点疑点
对曲线方程中参数范围的讨论,应注意应用函数、不等式等数学思想方法.
基础练习
7、过抛物线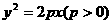 上一定点
上一定点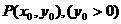 ,作两条直线交抛物线于
,作两条直线交抛物线于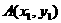 ,
,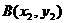
(1)求:抛物线上纵坐标为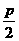 的点到焦点F的距离;
的点到焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求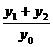 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com