
题目列表(包括答案和解析)
1. 已知实数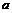 、
、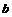 、
、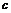 满足
满足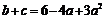 ,
,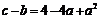 ,则
,则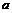 、
、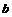 、
、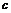 的大小关系是( )
的大小关系是( )
A.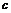 ≥
≥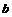 >
>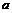 B.
B.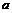 >
>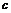 ≥
≥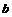 C.
C.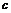 >
>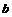 >
>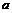 D.
D.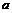 >
>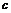 >
>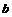
12.不等式的恒成立,能成立,恰成立等问题:不等式恒成立问题的常规处理方式?(常应用函数方程思想和“分离变量法”转化为最值问题,也可抓住所给不等式的结构特征,利用数形结合法)
1).恒成立问题
若不等式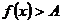 在区间
在区间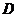 上恒成立,则等价于在区间
上恒成立,则等价于在区间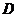 上
上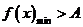
若不等式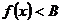 在区间
在区间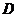 上恒成立,则等价于在区间
上恒成立,则等价于在区间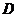 上
上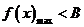
(1)设实数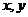 满足
满足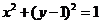 ,当
,当 时,
时,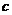 的取值范围是______
的取值范围是______
(答: );
);
(2)不等式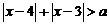 对一切实数
对一切实数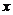 恒成立,求实数
恒成立,求实数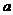 的取值范围_____
的取值范围_____
(答: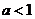 );
);
(3)若不等式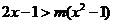 对满足
对满足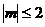 的所有
的所有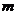 都成立,则
都成立,则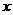 的取值范围_____
的取值范围_____
(答:(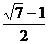 ,
,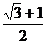 ));
));
(4)若不等式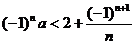 对于任意正整数
对于任意正整数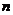 恒成立,则实数
恒成立,则实数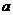 的取值范围是_____(答:
的取值范围是_____(答: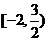 );
);
(5)若不等式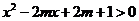 对
对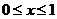 的所有实数
的所有实数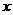 都成立,求
都成立,求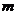 的取值范围.(答:
的取值范围.(答: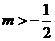 )
)
2). 能成立问题
若在区间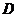 上存在实数
上存在实数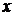 使不等式
使不等式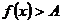 成立,则等价于在区间
成立,则等价于在区间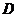 上
上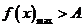 ;
;
若在区间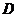 上存在实数
上存在实数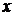 使不等式
使不等式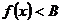 成立,则等价于在区间
成立,则等价于在区间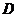 上的
上的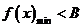 .
.
已知不等式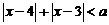 在实数集
在实数集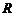 上的解集不是空集,求实数
上的解集不是空集,求实数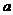 的取值范围______
的取值范围______
(答: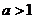 )
)
3). 恰成立问题
若不等式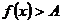 在区间
在区间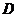 上恰成立, 则等价于不等式
上恰成立, 则等价于不等式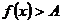 的解集为
的解集为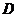 ;
;
若不等式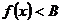 在区间
在区间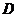 上恰成立, 则等价于不等式
上恰成立, 则等价于不等式
11.含绝对值不等式的性质:
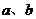 同号或有
同号或有
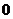
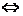
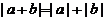
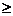
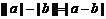 ;
;
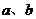 异号或有
异号或有
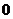
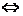
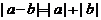
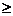
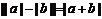 .
.
9、含参不等式的解法:求解的通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”注意解完之后要写上:“综上,原不等式的解集是…”。注意:按参数讨论,最后应按参数取值分别说明其解集;但若按未知数讨论,最后应求并集.
提醒:(1)解不等式是求不等式的解集,最后务必有集合的形式表示;
(2)不等式解集的端点值往往是不等式对应方程的根或不等式有意义范围的端点值。
8.绝对值不等式的解法:
(1)分段讨论法(最后结果应取各段的并集):
(2)利用绝对值的定义;
(3)数形结合
7.分式不等式的解法:分式不等式的一般解题思路是先移项使右边为0,再通分并将分子分母分解因式,并使每一个因式中最高次项的系数为正,最后用标根法求解。解分式不等式时,一般不能去分母,但分母恒为正或恒为负时可去分母。
6.简单的一元高次不等式的解法:
标根法:(1)分解成若干个一次因式的积,并使每一个因式中最高次项的系数为正;
(2)将每一个一次因式的根标在数轴上,从最大根的右上方依次通过每一点画曲线;并注意奇穿过偶弹回;
(3)根据曲线显现 的符号变化规律,写出不等式的解集。
的符号变化规律,写出不等式的解集。
5、证明不等式的方法:比较法、分析法、综合法和放缩法(比较法的步骤是:作差(商)后通过分解因式、配方、通分等手段变形判断符号或与1的大小,然后作出结论。).
常用的放缩技巧有: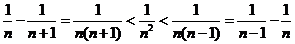
4.常用不等式有:
(1)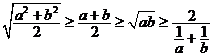 (根据目标不等式左右的运算结构选用) ;
(根据目标不等式左右的运算结构选用) ;
(2)a、b、c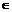 R,
R,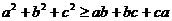 (当且仅当
(当且仅当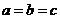 时,取等号);
时,取等号);
(3)若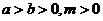 ,则
,则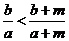 (糖水的浓度问题)。
(糖水的浓度问题)。
3.利用重要不等式求函数最值时,你是否注意到:“一正二定三相等,和定积最大,积定和最小”这17字方针。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com