
题目列表(包括答案和解析)
5.(天津理10)若函数 在区间
在区间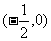 内单调递增,则a的取值范围是(A)
内单调递增,则a的取值范围是(A)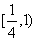 (B)
(B) 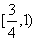 (C)
(C)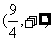 (D)
(D)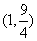 ( B )
( B )
4.(福建卷理12)f(x)是定义在R上的以3为周期的奇函数,且f(2)=0在区间(0,6)内解的个数的最小值是 A.2; B.3; C.4; D.5 ( D )
3.(全国卷I)已知函数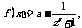 ,若
,若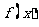 为奇函数,则
为奇函数,则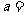 ________。
________。
解析:函数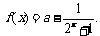 若
若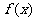 为奇函数,则
为奇函数,则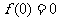 ,即
,即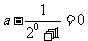 ,a=
,a=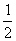 .
.
2.(全国卷I)已知函数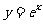 的图象与函数
的图象与函数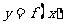 的图象关于直线
的图象关于直线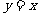 对称,则
对称,则
A.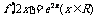 B.
B.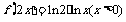
C.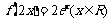 D.
D.
解:函数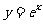 的图象与函数y=f(x)的图象关于直线
的图象与函数y=f(x)的图象关于直线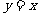 对称,所以f(x)是
对称,所以f(x)是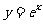 的反函数,即
的反函数,即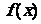 =
=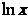 ,∴
,∴ 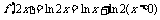 ,选D.
,选D.
1.. (北京卷)在下列四个函数中,满足性质:“对于区间(1,2)上的任意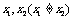 ,
,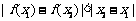 恒成立”的只有
恒成立”的只有
(A)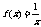 (B)
(B)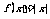 (C)
(C)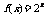 (D)
(D)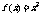
解: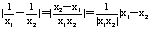 |
|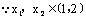
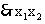 >1
>1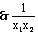 <1\
<1\ 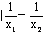 |<|x1-x2|故选A
|<|x1-x2|故选A
例1.(05浙江文20)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
(Ⅲ)若h(x)=g(x)-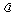 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数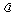 的取值范围。
的取值范围。
解:(Ⅰ)设函数y=f(x)的图象上任一点Q(xqλ,yq关于原点的对称点(x,y),
则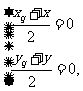 即
即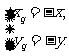 ∵点Qxq,yq)在函数f(x)的图象上,∴-y=-x2+2x.,故g(x)=-x2+2x
∵点Qxq,yq)在函数f(x)的图象上,∴-y=-x2+2x.,故g(x)=-x2+2x
(Ⅱ)由g(x)≥f(x)-|x-1|可得2x2-|x-1|≤0,当x≥1时,2x2-x+1≤0,此时不等式无解,
当x<1时,2x2+x-1≤0,∴-1≤x≤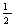 ,因此,原不等式的解集为[-1,
,因此,原不等式的解集为[-1, 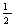 ]
]
(Ⅲ)h(x)=-(1+λ)x2+2(1-λ)x+1
① 当λ=-1时,h(x)=4x+1在[-1,1]上是增函数,∴λ=-1
②
 当λ≠-1时,对称轴的方程为x=
当λ≠-1时,对称轴的方程为x= .
.
(i)
当λ<-1时, 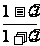 ≤-1,解得λ<-1.
≤-1,解得λ<-1.
(ii)
当λ>-1时, 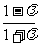 ≥-1,解得-1<λ≤0.
≥-1,解得-1<λ≤0.
综上,λ≤0
例2.(江苏卷)已知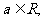 函数
函数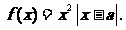 (Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
解:(1)当a=2时, ,则方程f(x)=x即为
,则方程f(x)=x即为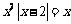
解方程得:
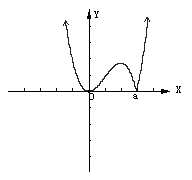
(2)(I)当a>0时,
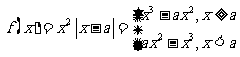 ,作出其草图见右, 易知f (x)有两个极值点
,作出其草图见右, 易知f (x)有两个极值点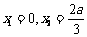 借助于图像可知,当
借助于图像可知,当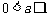 时,函数f (x)在区间[1,2]上为增函数,此时
时,函数f (x)在区间[1,2]上为增函数,此时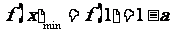
当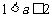 时,显然此时函数的最小值为
时,显然此时函数的最小值为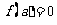
当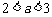 时,
时,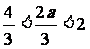 ,此时f(x)在区间
,此时f(x)在区间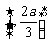 为增函数,在区间
为增函数,在区间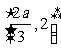 上为减函数,
上为减函数,
∴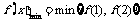 ,又可得
,又可得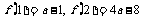 ∴
∴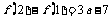
则当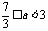 时,
时,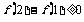 ,此时
,此时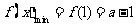
当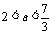 时,
时,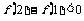 ,此时
,此时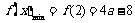
当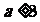 时,
时,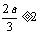 ,此时f(x)在区间[1,2]为增函数,故
,此时f(x)在区间[1,2]为增函数,故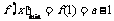
(II)当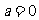 时,
时,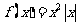 ,此时f(x)在区间[1,2]也为增函数,故
,此时f(x)在区间[1,2]也为增函数,故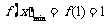
(III)当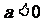 时,其草图见右 显然函数f(x)在区间[1,2]为增函数,故
时,其草图见右 显然函数f(x)在区间[1,2]为增函数,故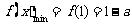
例3.(湖南卷)已知函数f(x)=lnx,g(x)=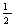 ax2+bx,a≠0.
ax2+bx,a≠0.
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
解:(I)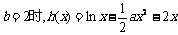 ,则
,则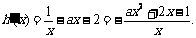
因为函数h(x)存在单调递减区间,所以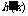 <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞).
(II)证法一 设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为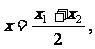
C1在点M处的切线斜率为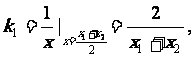
C2在点N处的切线斜率为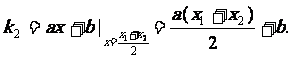
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2.
即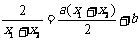 ,
,
则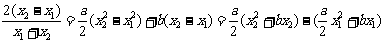
=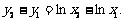
所以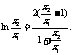 设
设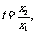 则
则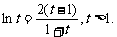 ①
①
令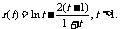 则
则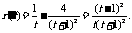
因为 时,
时,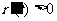 ,所以
,所以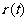 在
在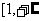 )上单调递增. 故
)上单调递增. 故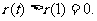
则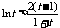 . 这与①矛盾,假设不成立. 故C1在点M处的切线与C2在点N处的切线不平行.
. 这与①矛盾,假设不成立. 故C1在点M处的切线与C2在点N处的切线不平行.
证法二:同证法一得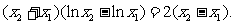 因为
因为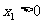 ,所以
,所以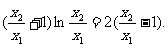
令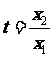 ,得
,得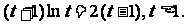 ②
②
令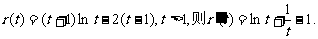
因为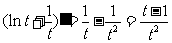 ,所以
,所以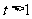 时,
时,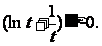
故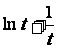 在[1,+
在[1,+ 上单调递增.从而
上单调递增.从而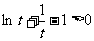 ,即
,即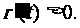
于是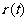 在[1,+
在[1,+ 上单调递增.
上单调递增.
故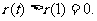 即
即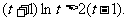 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
例4. 已知函数y=f (x)是定义在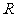 上的周期函数,周期T=5,函数
上的周期函数,周期T=5,函数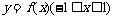 是奇函数
是奇函数 又知y=f (x)在[0,1]上是一次函数,在[1,4]上是二次函数,且在x=2时函数取得最小值
又知y=f (x)在[0,1]上是一次函数,在[1,4]上是二次函数,且在x=2时函数取得最小值 .
.
①证明: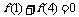 ;②求
;②求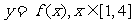 的解析式;③求
的解析式;③求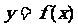 在[4,9]上的解析式.
在[4,9]上的解析式.
解:∵f (x)是以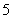 为周期的周期函数,∴
为周期的周期函数,∴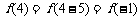 ,
,
又∵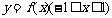 是奇函数,∴
是奇函数,∴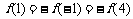 ,∴
,∴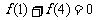

②当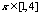 时,由题意可设
时,由题意可设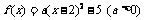 ,
,
由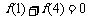 得
得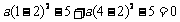 ,∴
,∴ ,
,
∴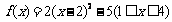

③∵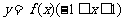 是奇函数,∴
是奇函数,∴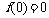 ,
,
又知y=f (x)在[0,1]上是一次函数,∴可设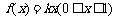 ,而
,而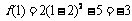 ,
,
∴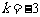 ,∴当
,∴当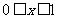 时,f (x)=-3x,
时,f (x)=-3x,
从而当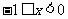 时,
时,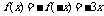 ,故
,故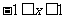 时,f (x)= -3x,.
时,f (x)= -3x,.
∴当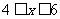 时,有
时,有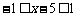 ,∴0.
,∴0.
当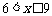 时,
时,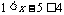 ,∴
,∴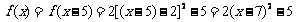
∴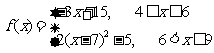
例5:已知函数f(x)在(-1,1)上有定义,f(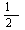 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(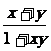 ),试证明:
(1)f(x)为奇函数;(2)f(x)在(-1,1)上单调递减.
……
),试证明:
(1)f(x)为奇函数;(2)f(x)在(-1,1)上单调递减.
……
证明: (1)由f(x)+f(y)=f(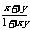 )可令x=y=0,得f(0)=0,
)可令x=y=0,得f(0)=0,
令y=-x,得f(x)+f(-x)=f(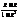 )=f(0)=0. ∴f(x)=-f(-x). ∴f(x)为奇函数.
)=f(0)=0. ∴f(x)=-f(-x). ∴f(x)为奇函数.
(2)先证f(x)在(0,1)上单调递减.
令0<x1<x2<1,则f(x2)-f(x1)=f(x2)+f(-x1)=f(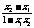 )
)
∵0<x1<x2<1,∴x2-x1>0,1-x1x2>0,∴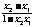 >0,
>0,
又(x2-x1)-(1-x2x1)=(x2-1)(x1+1)<0,∴x2-x1<1-x2x1,∴0<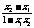 <1,由题意知f(
<1,由题意知f(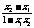 )<0,
)<0,
即 f(x2)<f(x1).
∴f(x)在(0,1)上为减函数,又f(x)为奇函数且f(0)=0 ∴f(x)在(-1,1)上为减函数.
∴f(x)在(-1,1)上为减函数.
例6.(湖南卷)设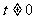 ,点P(t,0)是函数
,点P(t,0)是函数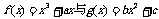 的图象的一个公共点,两函数的图象在点P处有相同的切线.(Ⅰ)用t表示a,b,c;
的图象的一个公共点,两函数的图象在点P处有相同的切线.(Ⅰ)用t表示a,b,c;
(Ⅱ)若函数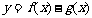 在(-1,3)上单调递减,求t的取值范围.
在(-1,3)上单调递减,求t的取值范围.
解:(I)因为函数f (x),g(x)的图象都过点((t,0),所以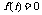 ,
,
即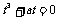 .因为
.因为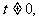 所以
所以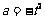 .
. 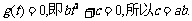
又因为f (x),g(x)在点(t,0)处有相同的切线,所以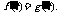
而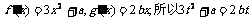
将 代入上式得
代入上式得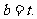 因此
因此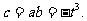 故
故 ,
,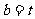 ,
,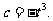
(II)解法一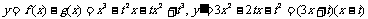 .
.
当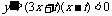 时,函数y= f (x)-g(x)单调递减.
时,函数y= f (x)-g(x)单调递减.
由 ,若
,若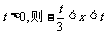 ;若
;若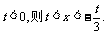
由题意,函数y= f (x)-g(x)在(-1,3)上单调递减,
则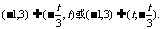 所以
所以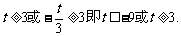
又当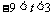 时,函数y= f (x)-g(x)在(-1,3)上单调递减.
时,函数y= f (x)-g(x)在(-1,3)上单调递减.
所以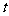 的取值范围为
的取值范围为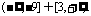
解法二: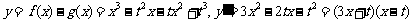
因为函数y= f (x)-g(x)在(-1,3)上单调递减,且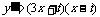 是(-1,3)上的抛物线,
是(-1,3)上的抛物线,
所以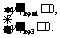 即
即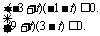 所以
所以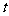 的取值范围为
的取值范围为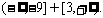
12.(天津文9)若函数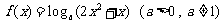 在区间
在区间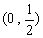 内恒有
内恒有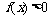 ,则
,则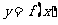 的单调递增区间为
的单调递增区间为
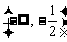
11.设f(x)是定义在R上的奇函数,且y=f(x)的图象关于直线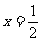 对称,则f(1)+f(2)+f(3)+f(4)+f(5)=
0
。
对称,则f(1)+f(2)+f(3)+f(4)+f(5)=
0
。
10.直线沿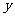 轴正方向平移
轴正方向平移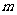
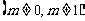 个单位,再沿
个单位,再沿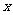 轴负方向平移
轴负方向平移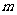 -1个单位得直线
-1个单位得直线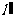 ,若直线
,若直线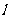 与
与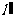 重合,则直线
重合,则直线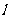 的斜率为( )
的斜率为( )
(A) 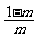 (B)
(B)  (C)
(C) 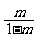 (D)
(D) 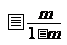
9.设f(x),g(x)分别是定义在R上的奇函数和偶函数,当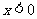 时,
时,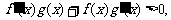 且g(-3)=0则不等式f(x)g(x)<0的解集是 ( )
且g(-3)=0则不等式f(x)g(x)<0的解集是 ( )
A.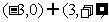 B.
B.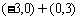 C.
C.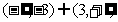 D.
D.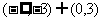
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com