
题目列表(包括答案和解析)
2. 不等式大小比较的常用方法:(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;(2)作商(常用于分数指数幂的代数式);(3)分析法;(4)平方法;(5)分子(或分母)有理化;(6)利用函数的单调性;(7)寻找中间量或放缩法 ;(8)图象法。其中比较法(作差、作商)是最基本的方法。
1、不等式的性质:
(1)同向不等式可以相加;异向不等式可以相减:若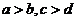 ,则
,则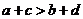 (若
(若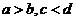 ,则
,则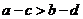 ),但异向不等式不可以相加;同向不等式不可以相减;
),但异向不等式不可以相加;同向不等式不可以相减;
(2)左右同正不等式:同向的不等式可以相乘,但不能相除;异向不等式可以相除,但不能相乘:若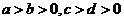 ,则
,则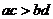
若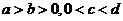 ,则
,则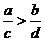 ;
;
(3)左右同正不等式:两边可以同时乘方或开方:若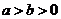 ,则
,则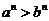 或
或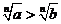 ;
;
(4)若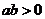 ,
,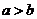 ,则
,则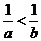 ;若
;若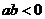 ,
,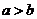 ,则
,则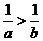 。
。
5.指数不等式与对数不等式
(1)当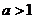 时,
时,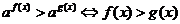 ;
;
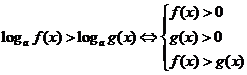 .
.
(2)当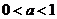 时,
时,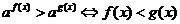 ;
;
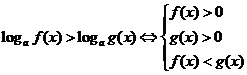
4.含有绝对值的不等式 当a> 0时,有
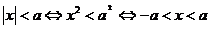 .
.
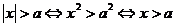 或
或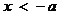 .
.
3.一元二次不等式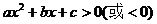
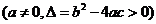 ,
,
如果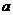 与
与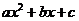 同号,则其解集在两根之外;如果
同号,则其解集在两根之外;如果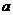 与
与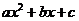 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
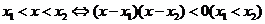 ;
;
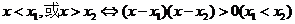 .
.
2.极值定理
已知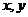 都是正数,则有
都是正数,则有
(1)若积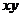 是定值
是定值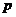 ,则当
,则当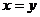 时和
时和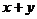 有最小值
有最小值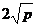 ;
;
(2)若和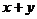 是定值
是定值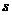 ,则当
,则当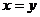 时积
时积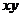 有最大值
有最大值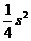 .
.
1.常用不等式:
(1)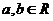
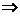
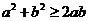 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(2)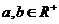
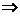
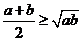 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(3)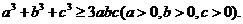
(4)柯西不等式
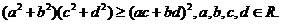
(5)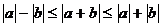 .
.
(1)理解不等式的性质及其证明.
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
(3)掌握分析法、综合法、比较法证明简单不等式.
(4)掌握简单不等式的解法.
(5)理解│a│-│b│≤│a+b│≤│a│+│b│
[注意]不等式在数学的各个分支中都有广泛的应用,同时还是继续学习高等数学的基础.纵观历年试题,涉及不等式内容的考题大致可分为以下几类:①不等式的证明;②解不等式;③取值范围的问题;④应用题.
22.(本小题满分14分)
已知函数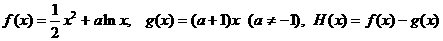 。
。
(1) 若函数f(x)、g(x)在区间[1,2]上都为单调函数且它们的单调性相同,求实数a的取值范围;
(2)
a、b是函数H(x)的两个极值点,a<b,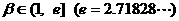 。求证:对任意的x1、x2
。求证:对任意的x1、x2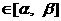 ,不等式
,不等式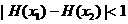 成立。
成立。




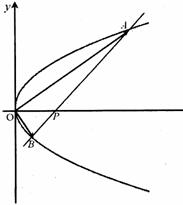


21.(本小题满分12分)
已知抛物线的方程为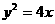 ,过点P(2,0)的直线l与抛物线交于A、B两点,点Q满足
,过点P(2,0)的直线l与抛物线交于A、B两点,点Q满足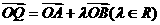 。
。
(1)
当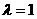 时,求点Q的轨迹方程;
时,求点Q的轨迹方程;
(2)
若点Q在x轴上,且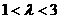 ,求直线l的斜率k的取值范围。
,求直线l的斜率k的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com