
题目列表(包括答案和解析)
1.设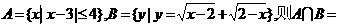 ( )
( )
A.{0} B.{2} C.φ D.{x|2≤x≤7}
15.(江安中学)已知函数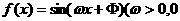 ≤
≤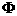 ≤
≤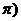 是R上的偶函数,其图像关于点M
是R上的偶函数,其图像关于点M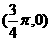 对称,且在区间[0,
对称,且在区间[0,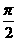 ]上是单调函数,求
]上是单调函数,求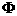 和
和 的值。
的值。
正解:由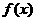 是偶函数,得
是偶函数,得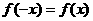
故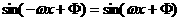
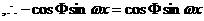
对任意x都成立,且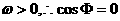
依题设0≤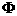 ≤
≤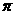 ,
,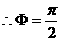
由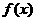 的图像关于点M对称,得
的图像关于点M对称,得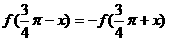
取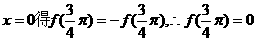

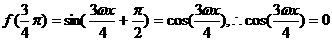
又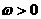 ,得
,得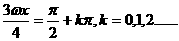
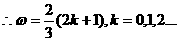
当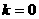 时,
时,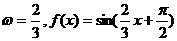 在
在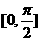 上是减函数。
上是减函数。
当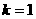 时,
时,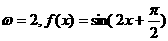 在
在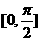 上是减函数。
上是减函数。
当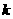 ≥2时,
≥2时,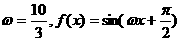 在
在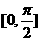 上不是单调函数。
上不是单调函数。
所以,综合得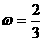 或
或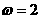 。
。
误解:①常见错误是未对K进行讨论,最后 只得一解。
只得一解。
②对题目条件在区间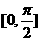 上是单调函数,不进行讨论,故对
上是单调函数,不进行讨论,故对 ≥
≥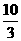 不能排除。
不能排除。
欢迎访问
14.(蒲中)已知函数f(x)=-sin2x+sinx+a,(1)当f(x)=0有实数解时,求a的取值范围;(2)若x∈R,有1≤f(x)≤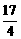 ,求a的取值范围。
,求a的取值范围。
解:(1)f(x)=0,即a=sin2x-sinx=(sinx-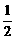 )2-
)2-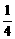
∴当sinx=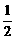 时,amin=
时,amin=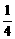 ,当sinx=-1时,amax=2,
,当sinx=-1时,amax=2,
∴a∈[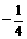 ,2]为所求
,2]为所求
(2)由1≤f(x)≤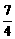 得
得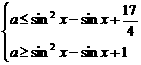
∵ u1=sin2x-sinx+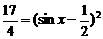 +4≥4
+4≥4
u2=sin2x-sinx+1=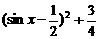 ≤3
≤3
∴ 3≤a≤4
点评:本题的易错点是盲目运用“△”判别式。
13.(薛中)求函数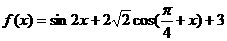 的值域
的值域
答案:原函数可化为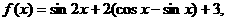 设
设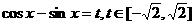 则
则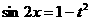 则
则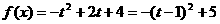
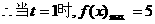 ,
,
当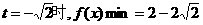
错解: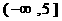
错因:不考虑换元后新元t的范围。
12.(丁中)(本小题满分12分)
设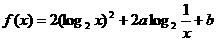 ,已知
,已知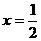 时
时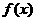 有最小值-8。
有最小值-8。
(1)、求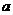 与
与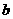 的值。(2)求满足
的值。(2)求满足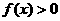 的
的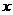 的集合A。
的集合A。
错解: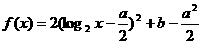 ,当
,当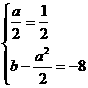 时,得
时,得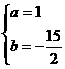
错因:没有注意到应是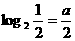 时,
时,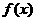 取最大值。
取最大值。
正解: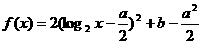 ,当
,当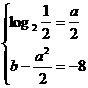 时,得
时,得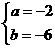
11.(磨中)已知Sinx+Siny=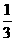 ,求Siny-cos2x的最大值。
,求Siny-cos2x的最大值。
正确答案: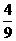
错误原因:挖掘隐含条件
10.(磨中)求函数y=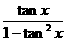 的最小正周期
的最小正周期
正确答案:最小正周期π
错误原因:忽略对函数定义域的讨论。
9.(磨中)求函数y=Sin(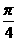 -3x)的单调增区间:
-3x)的单调增区间:
正确答案:增区间[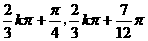 ](
](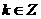 )
)
错误原因:忽视t=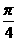 -3x为减函数
-3x为减函数
8.(磨中)已知Sinα=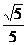 Sinβ=
Sinβ=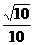 ,且α,β为锐角,求α+β的值。
,且α,β为锐角,求α+β的值。
正确答案:α+β=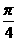
错误原因:要挖掘特征数值来缩小角的范围
7.(搬中) 求函数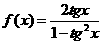 的最小正周期。
的最小正周期。
解:函数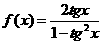 的定义域要满足两个条件;
的定义域要满足两个条件;
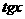 要有意义且
要有意义且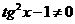
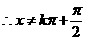 ,且
,且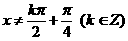
当原函数式变为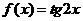 时,
时,
此时定义域为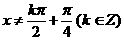
显然作了这样的变换之后,定义域扩大了,两式并不等价
所以周期未必相同,那么怎么求其周期呢?首先作出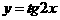 的图象:
的图象:
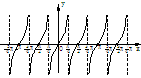
而原函数的图象与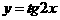 的图象大致相同
的图象大致相同
只是在上图中去掉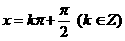 所对应的点
所对应的点
从去掉的几个零值点看,原函数的周期应为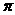
说明:此题极易由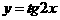 的周期是
的周期是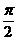 而得出原函数的周期也是
而得出原函数的周期也是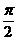 ,这是错误的,原因正如上所述。那么是不是说非等价变换周期就不同呢?也不一定,如1993年高考题:函数
,这是错误的,原因正如上所述。那么是不是说非等价变换周期就不同呢?也不一定,如1993年高考题:函数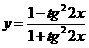 的最小正周期是( )。A.
的最小正周期是( )。A.
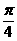 B.
B. 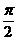 C.
C.
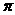 D.
D. 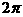 。此题就可以由
。此题就可以由 的周期为
的周期为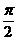 而得原函数的周期也是
而得原函数的周期也是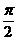 。但这个解法并不严密,最好是先求定义域,再画出图象,通过空点来观察,从而求得周期。
。但这个解法并不严密,最好是先求定义域,再画出图象,通过空点来观察,从而求得周期。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com