
题目列表(包括答案和解析)
13.函数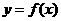 的图象的对称性
的图象的对称性
(1)函数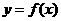 的图象关于直线
的图象关于直线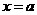 对称
对称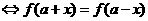
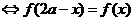 .
.
(2)函数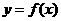 的图象关于直线
的图象关于直线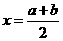 对称
对称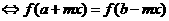
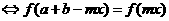 .
.
12.多项式函数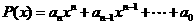 的奇偶性
的奇偶性
多项式函数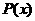 是奇函数
是奇函数
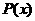 的偶次项(即奇数项)的系数全为零.
的偶次项(即奇数项)的系数全为零.
多项式函数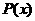 是偶函数
是偶函数
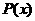 的奇次项(即偶数项)的系数全为零.
的奇次项(即偶数项)的系数全为零.
11.若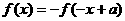 ,则函数
,则函数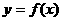 的图象关于点
的图象关于点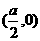 对称; 若
对称; 若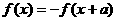 ,则函数
,则函数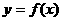 为周期为
为周期为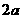 的周期函数.
的周期函数.
10.对于函数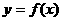 (
( ),
),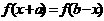 恒成立,则函数
恒成立,则函数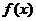 的对称轴是函数
的对称轴是函数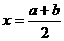 ;两个函数
;两个函数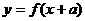 与
与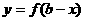 的图象关于直线
的图象关于直线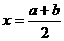 对称.
对称.
9.若函数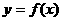 是偶函数,则
是偶函数,则
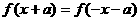 ;若函数
;若函数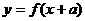 是偶函数,则
是偶函数,则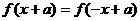 .
.
8.奇偶函数的图象特征
奇函数的图象关于原点对称,偶函数的图象关于y轴对称;反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y轴对称,那么这个函数是偶函数.
7.如果函数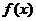 和
和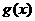 都是减函数,则在公共定义域内,和函数
都是减函数,则在公共定义域内,和函数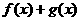 是减函数; 如果函数
是减函数; 如果函数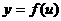 和
和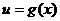 在其对应的定义域上都是减函数,则复合函数
在其对应的定义域上都是减函数,则复合函数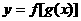 是增函数.
是增函数.
7.函数的单调性
(1)设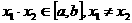 那么
那么
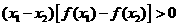

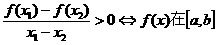 上是增函数;
上是增函数;
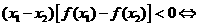
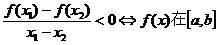 上是减函数.
上是减函数.
(2)设函数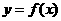 在某个区间内可导,如果
在某个区间内可导,如果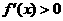 ,则
,则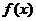 为增函数;如果
为增函数;如果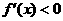 ,则
,则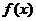 为减函数.
为减函数.
6.定区间上含参数的二次不等式恒成立的条件依据(1)在给定区间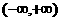 的子区间
的子区间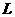 (形如
(形如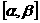 ,
,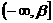 ,
,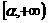 不同)上含参数的二次不等式
不同)上含参数的二次不等式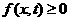 (
(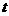 为参数)恒成立的充要条件是
为参数)恒成立的充要条件是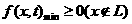 .
.
(2)在给定区间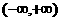 的子区间上含参数的二次不等式
的子区间上含参数的二次不等式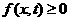 (
(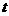 为参数)恒成立的充要条件是
为参数)恒成立的充要条件是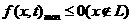 .
.
(3)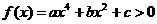 恒成立的充要条件是
恒成立的充要条件是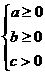 或
或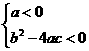 .
.
5.一元二次方程的实根分布
依据:若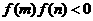 ,则方程
,则方程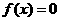 在区间
在区间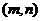 内至少有一个实根 .
内至少有一个实根 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com