
题目列表(包括答案和解析)
11.用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻折900角,再焊接而成,问该容器的高为多少时,容器的容积最大?最大的容积是多少?
解:设容器的高为x,容器的体积为V.
则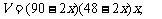 (0 < x < 24)
(0 < x < 24)
=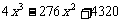 x
x
∵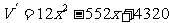 x
x
由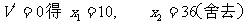
∴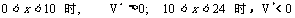
所以 当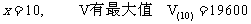
又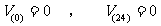
所以 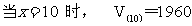 0
0
答:该容器的高为10cm时,容器有最大容积19600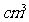
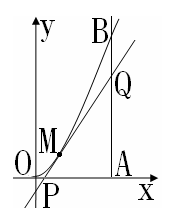
10.如图,曲线段OMB是函数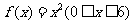 的图象,
的图象,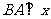 轴于点A,曲线段OMB上一点M
轴于点A,曲线段OMB上一点M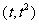 处的切线PQ交x轴于点P,交线段AB于点Q
处的切线PQ交x轴于点P,交线段AB于点Q
(1)若t已知,求切线PQ的方程 (2)求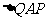 的面积的最大值
的面积的最大值
 解:(1)
解:(1)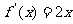 ,所以过点M的切线的斜率为
,所以过点M的切线的斜率为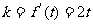
由点斜式得切线PQ方程为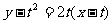 ,
,
即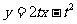 ……①
……①
(2)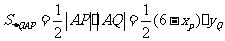 …………②
…………②
对①令x=6得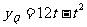 …………③
…………③
令y=0得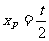 …………④
…………④
③④代入②得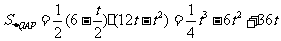
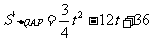 ,令
,令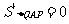 解得
解得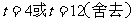
|
T |
(0,4) |
4 |
(4,6) |
|
S’ |
+ |
0 |
- |
|
S |
增 |
极大值64 |
减 |
所以当t=4时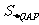 有极大值64,
有极大值64,
所以当t=4时,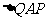 的面积的最大值为64.
的面积的最大值为64.
9. 函数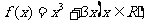 若
若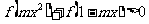 恒成立,求实数
恒成立,求实数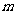 的取值范围
的取值范围
解:由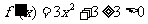 ,得
,得
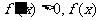 单调递增;
单调递增;
又
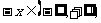
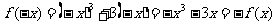 ,
,
所以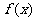 是奇函数.
是奇函数.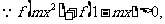
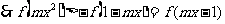 ,
,

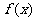 在
在 上单调递增,
上单调递增,  恒成立,即:
恒成立,即: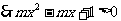 恒成立,分类:①当
恒成立,分类:①当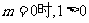 恒成立,
恒成立,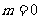 适合;
适合;
②当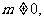
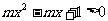 恒成立
恒成立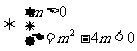 解得:
解得: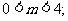
综上,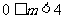
说明:(1)通过研究函数的性质(单调性与奇偶性),利用函数的性质解决不等式问题,是函数思想的重要应用.(2)找寻使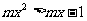 恒成立的条件实际上依然用的是函数图像(数形结合)的函数思想.
恒成立的条件实际上依然用的是函数图像(数形结合)的函数思想.
变式:设函数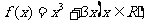 若
若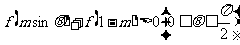 恒成立,求实数
恒成立,求实数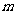 的取值范围.
的取值范围.
解:由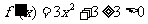 ,得
,得
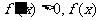 单调递增;
单调递增;
又
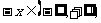
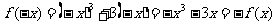 ,
,
所以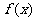 是奇函数.
是奇函数.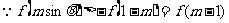 ,
,
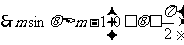 恒成立,即
恒成立,即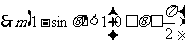 恒成立.
恒成立.
①当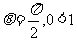 成立;
成立;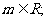 ②当
②当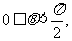
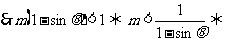
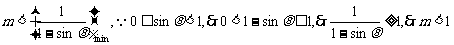
8.人教版选修1-1第108页B 组习题,选修2-2第34页B组习题
利用函数的单调性,证明: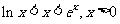
变式1:证明: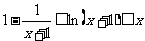 ,
,
证明:(1)构造函数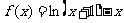 ,
,
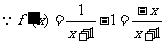
 ,当
,当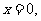
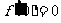 ,得下表
,得下表
|
|
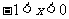 |
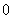 |
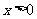 |
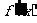 |
+ |
0 |
- |
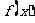 |
单调递增 |
极大值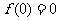 |
单调递减 |
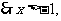 总有
总有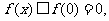
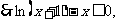
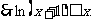
另解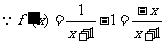
 ,当
,当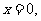
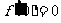 ,
,
当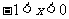 ,
,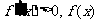 单调递增,
单调递增,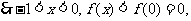 ……①
……①
当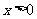 ,
,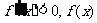 单调递减,
单调递减,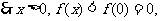 ………………②
………………②
当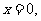
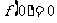 …………………………………………………………③
…………………………………………………………③
综合①②③得:当 时,
时,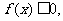
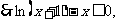
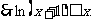
(2)构造函数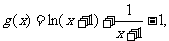
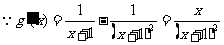 ,
,
当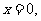
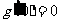 ,当
,当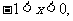
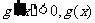 单调递减;
单调递减;
当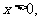
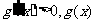 单调递增;
单调递增;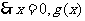 极小值=
极小值=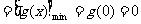 ,
,
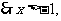 总有
总有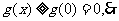
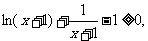 即:
即: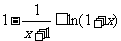 .
.
综上(1)(2)不等式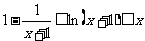 成立.
成立.
变式:(理科)设函数f(x)=(1+x)2-ln(1+x)2.若关于x的方程f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,求实数a的取值范围.
解:
方程f(x)=x2+x+a, 即x-a+1-ln(1+x)2=0,记g(x)=x-a+1-ln(1+x)2.
所以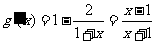 .由
.由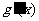 >0,得x<-1或x>1,由
>0,得x<-1或x>1,由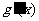 <0
<0
得-1<x<1.
所以g(x)在[0,1]上递减,在[1,2]上递增,为使f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,只须g(x)=0在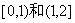 上各有一个实根,于是有
上各有一个实根,于是有

2.应用导数解决实际问题,关键是要建立恰当的数学模型(函数关系),如果函数在区间内只有一个点使 (x)=0,此时函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值.
(x)=0,此时函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值.
拓展题例
[例1] 函数y=2x3+3x2-12x+14在[-3,4]上的最大值为________,最小值为________.
解析:y′=6x2+6x-12=0.
x=1,-2,f(-3)=20,f(-2)=34,f(1)=7,f(4)=142.
答案:142 7
[例2] 设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点.
(1)求常数a、b;
(2)判断x=-2,x=4是函数f(x)的极大值点还是极小值点,并说明理由.
解:(1) (x)=3x2+2ax+b.
(x)=3x2+2ax+b.
由极值点的必要条件可知x=-2和x=4是方程 (x)=0的两根,则a=-3,b=-24.
(x)=0的两根,则a=-3,b=-24.
(2) (x)=3(x+2)(x-4),得
(x)=3(x+2)(x-4),得
当x<-2时, (x)>0;
(x)>0;
当-2<x<4时, (x)<0.
(x)<0.
∴x=-2是f(x)的极大值点.
当x>4时, (x)>0,则x=4是f(x)的极小值点.
(x)>0,则x=4是f(x)的极小值点.
1.导数的基本应用如下表:

4.体会数形结合、函数、方程思想在本章的运用.
●教师下载中心
教学点睛
3.注意极值与最值的关系,理解若只有一个极值则必为最值.
2.函数f(x)在极值点不一定可导,如函数y=|x|在x=0处.
1. (x0)=0是x0为可导函数f(x)的极值点的必要不充分条件,如函数y=x3在x=0处.
(x0)=0是x0为可导函数f(x)的极值点的必要不充分条件,如函数y=x3在x=0处.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com