
题目列表(包括答案和解析)
9.(磨中)已知数列-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,则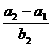 的值为___________。
的值为___________。
A、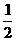 B、-
B、-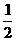 C、
C、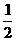 或-
或-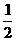 D、
D、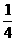
正确答案:A
错误原因:忽略b2为等比数列的第三项,b2符号与-1、-4同号
8.(磨中)已知Sk表示{an}的前K项和,Sn-Sn+1=an(n∈N+),则{an}一定是_______。
A、等差数列 B、等比数列 C、常数列 D、以上都不正确
正确答案:D
错误原因:忽略an=0这一特殊性
7.(搬中)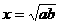 是
是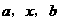 成等比数列的( )
成等比数列的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解: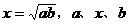 不一定等比
不一定等比
如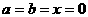
若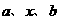 成等比数列
成等比数列
则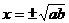
 选D
选D
说明:此题易错选为A或B或C,原因是等比数列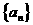 中要求每一项及公比
中要求每一项及公比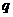 都不为零。
都不为零。
6.(搬中)一个只有有限项的等差数列,它的前5项的和为34,最后5项的和为146,所有项的和为234,则它的第七项等于( )
A. 22 B. 21 C. 19 D. 18
解:设该数列有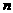 项
项
且首项为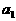 ,末项为
,末项为 ,公差为
,公差为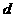
则依题意有
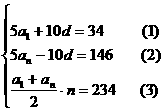
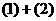 可得
可得
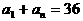
代入(3)有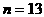
从而有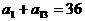
又所求项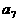 恰为该数列的中间项,
恰为该数列的中间项,
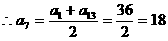
故选D
说明:虽然依题意只能列出3个方程,而方程所涉及的未知数有4个,但将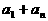 作为一个整体,问题即可迎刃而解。在求
作为一个整体,问题即可迎刃而解。在求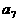 时,巧用等差中项的性质也值得关注。知识的灵活应用,来源于对知识系统的深刻理解。
时,巧用等差中项的性质也值得关注。知识的灵活应用,来源于对知识系统的深刻理解。
5.(石庄中学)某人为了观看2008年奥运会,从2001年起每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并且每年到期的存款及利息均自动转为新一年定期,到2008年将所有的存款和利息全部取回,则可取回的钱的总数(元)为( ).
A a(1+p)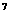 B a(1+p)
B a(1+p)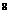 C
C 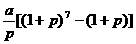 D
D 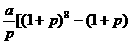 ]
]
正确答案:D 错因: 学生对存款利息的计算方法没掌握。
4.(石庄中学)已知非常数数列{a },满足 a
},满足 a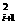 -a
-a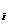 a
a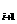 +a
+a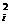 =0且a
=0且a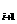 ≠a
≠a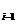 , i=1、2、3、…n,对于给定的正整数n,a
, i=1、2、3、…n,对于给定的正整数n,a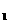 =a
=a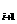 ,则
,则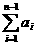
 等于( )
等于( )
A 2 B -1 C 1 D 0
正确答案:D 错因:学生看不懂题目,不能挖掘题目的隐含条件,{a }的项具有周期性。
}的项具有周期性。
3.(石庄中学)设{a }是等差数列,{b
}是等差数列,{b }为等比数列,其公比q≠1,
且b
}为等比数列,其公比q≠1,
且b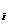 >0(i=1、2、3 …n) 若a
>0(i=1、2、3 …n) 若a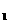 =b
=b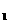 ,a
,a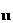 =b
=b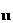 则 ( )
则 ( )
A a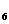 =b
=b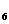 B a
B a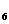 >b
>b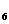 C a
C a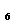 <b
<b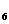 D a
D a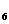 >b
>b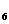 或 a
或 a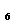 <b
<b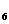
正确答案 B 错因:学生不能灵活运用等差中项和等比中项的定义及基本不等式。
2.(石庄中学)已知s 是等差数列{a
是等差数列{a }的前n项和,若a
}的前n项和,若a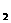 +a
+a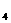 +a
+a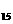 是一个确定的常数,则数列{s
是一个确定的常数,则数列{s }中是常数的项是( )
}中是常数的项是( )
A s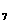 B s
B s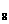 C s
C s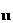 D s
D s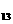
正确答案: D 错因:学生对等差数列通项公式的逆向使用和等差数列的性质不能灵活应用。
1.(石庄中学)设s 是等差数列{a
是等差数列{a }的前n项和,已知s
}的前n项和,已知s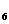 =36,
=36, s
s =324, s
=324, s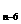 =144 (n>6),则n=( )
=144 (n>6),则n=( )
A 15 B 16 C 17 D 18
正确答案:D 错因:学生不能运用数列的性质计算a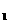 +a
+a =
=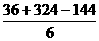
30.(本题满分10分)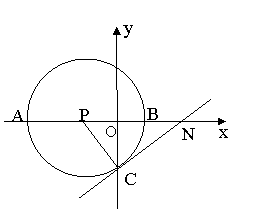 在平面直角坐标系中,坐标原点O,A点坐标为(-8。0)B点坐标为(2、0)以AB的中点P为圆心,AB为直径作
在平面直角坐标系中,坐标原点O,A点坐标为(-8。0)B点坐标为(2、0)以AB的中点P为圆心,AB为直径作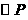 与Y轴的负半轴交于点C.
与Y轴的负半轴交于点C.
1) 求图象经过A、B、C三点的抛物线的函数关系式.
2) 设M为(1)中抛物线的顶点,求直线MC的关系式.
3)
试说明直线MC与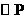 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com