
题目列表(包括答案和解析)
2.将函数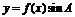 的图象向右平移
的图象向右平移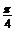 个单位后,再作关于
个单位后,再作关于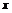 轴对称的曲线,得到函数
轴对称的曲线,得到函数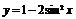 , 则
, 则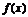 是
( )
是
( )
A.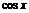 B.
B.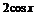 C.
C.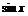 D.
D.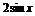
1.已知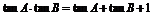 ,则
,则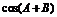 的值是 ( )
的值是 ( )
A.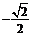 B.
B. 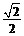 C.
C.
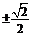 D.
D.
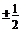
6. 已知函数y=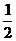 cos2x+
cos2x+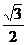 sinx·cosx+1 (x∈R),
sinx·cosx+1 (x∈R),
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图像可由y=sinx(x∈R)的图像经过怎样的平移和伸缩变换得到?
解:(1)y=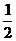 cos2x+
cos2x+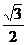 sinx·cosx+1=
sinx·cosx+1=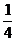 (2cos2x-1)+
(2cos2x-1)+ 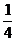 +
+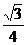 (2sinx·cosx)+1
(2sinx·cosx)+1
=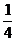 cos2x+
cos2x+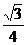 sin2x+
sin2x+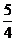 =
=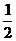 (cos2x·sin
(cos2x·sin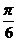 +sin2x·cos
+sin2x·cos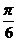 )+
)+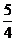
=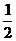 sin(2x+
sin(2x+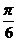 )+
)+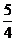
所以y取最大值时,只需2x+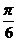 =
=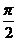 +2kπ,(k∈Z),即
x=
+2kπ,(k∈Z),即
x=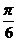 +kπ,(k∈Z)。
+kπ,(k∈Z)。
所以当函数y取最大值时,自变量x的集合为{x|x=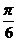 +kπ,k∈Z}
+kπ,k∈Z}
(2)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图像向左平移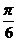 ,得到函数y=sin(x+
,得到函数y=sin(x+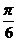 )的图像;
)的图像;
(ii)把得到的图像上各点横坐标缩短到原来的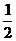 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+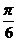 )的图像;
)的图像;
(iii)把得到的图像上各点纵坐标缩短到原来的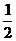 倍(横坐标不变),得到函数y=
倍(横坐标不变),得到函数y=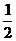 sin(2x+
sin(2x+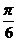 )的图像;
)的图像;
(iv)把得到的图像向上平移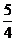 个单位长度,得到函数y=
个单位长度,得到函数y=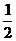 sin(2x+
sin(2x+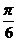 )+
)+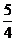 的图像。
的图像。
综上得到y=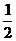 cos2x+
cos2x+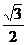 sinxcosx+1的图像。
sinxcosx+1的图像。
5.已知函数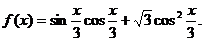
(Ⅰ)将f(x)写成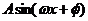 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
解: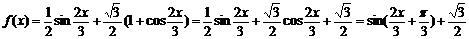
(Ⅰ)由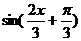 =0即
=0即
即对称中心的横坐标为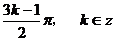
(Ⅱ)由已知b2=ac
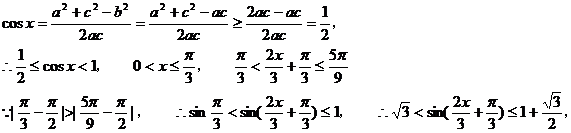 即
即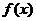 的值域为
的值域为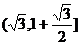 .
.
综上所述,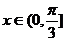 ,
,
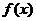 值域为
值域为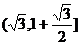 .
.
说明:本题综合运用了三角函数、余弦定理、基本不等式等知识,还需要利用数形结合的思想来解决函数值域的问题,有利于培养学生的运算能力,对知识进行整合的能力。
4.(重庆卷)设函数f(x)=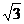 cos2ωx+sin
cos2ωx+sin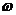 xcos
xcos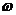 x+a(其中
x+a(其中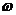 >0,a
>0,a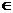 R),且f(x)的图象在y轴右侧的第一个高点的横坐标为
R),且f(x)的图象在y轴右侧的第一个高点的横坐标为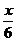 .(Ⅰ)求ω的值;(Ⅱ)如果f(x)在区间
.(Ⅰ)求ω的值;(Ⅱ)如果f(x)在区间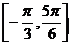 上的最小值为
上的最小值为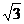 ,求a的值.
,求a的值.
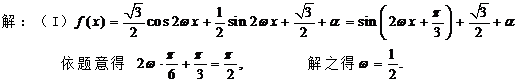
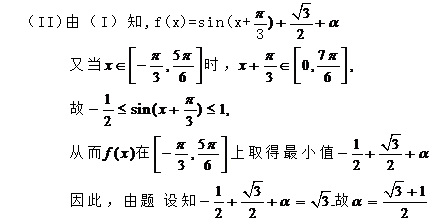
3.(上海春)已知函数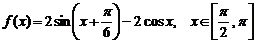 .
.
(1)若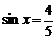 ,求函数
,求函数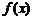 的值; (2)求函数
的值; (2)求函数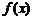 的值域.
的值域.
解:(1)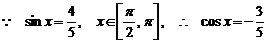 ,
,
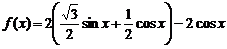
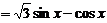
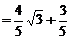 .
.
(2)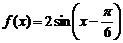
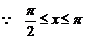
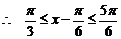 ,
, 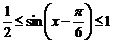 ,
,
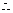 函数
函数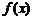 的值域为
的值域为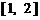 .
.
2.已知函数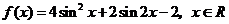 。
。
(1)求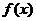 的最小正周期、
的最小正周期、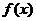 的最大值及此时x的集合;
的最大值及此时x的集合;
(2)证明:函数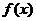 的图像关于直线
的图像关于直线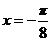 对称。
对称。
解: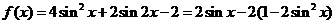
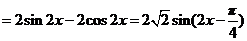
(1)所以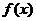 的最小正周期
的最小正周期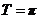 ,因为
,因为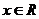 ,
,
所以,当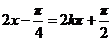 ,即
,即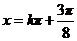 时,
时,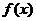 最大值为
最大值为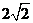 ;
;
(2)证明:欲证明函数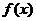 的图像关于直线
的图像关于直线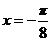 对称,只要证明对任意
对称,只要证明对任意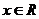 ,有
,有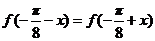 成立,
成立,
因为 ,
,
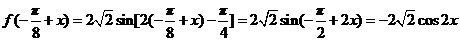 ,
,
所以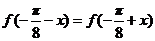 成立,从而函数
成立,从而函数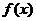 的图像关于直线
的图像关于直线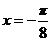 对称。
对称。
1.(广东卷)已知函数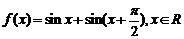 .(I)求
.(I)求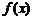 的最小正周期;
的最小正周期;
(II)求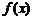 的的最大值和最小值;(III)若
的的最大值和最小值;(III)若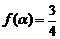 ,求
,求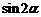 的值.
的值.
解: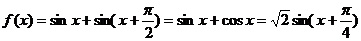
(Ⅰ)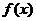 的最小正周期为
的最小正周期为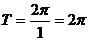 ; (Ⅱ)
; (Ⅱ)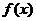 的最大值为
的最大值为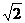 和最小值
和最小值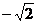 ;
;
(Ⅲ)因为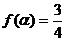 ,即
,即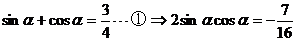 ,即
,即 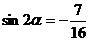
例1.已知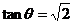 ,求(1)
,求(1)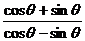 ;(2)
;(2)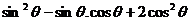 的值.
的值.
解:(1)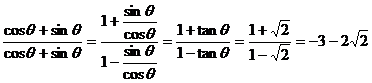 ;
;
(2) 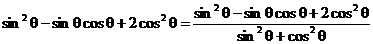
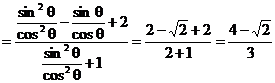 .
.
说明:利用齐次式的结构特点(如果不具备,通过构造的办法得到),进行弦、切互化,就会使解题过程简化。
例2.求函数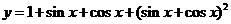 的值域。
的值域。
解:设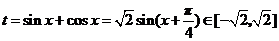 ,则原函数可化为
,则原函数可化为
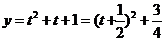 ,因为
,因为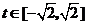 ,所以
,所以
当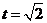 时,
时,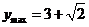 ,当
,当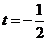 时,
时,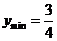 ,
,
所以,函数的值域为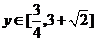 。
。
例3.已知函数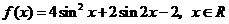 。
。
(1)求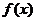 的最小正周期、
的最小正周期、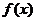 的最大值及此时x的集合;
的最大值及此时x的集合;
(2)证明:函数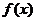 的图像关于直线
的图像关于直线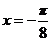 对称。
对称。
解: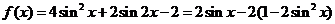
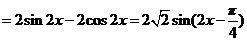
(1)所以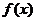 的最小正周期
的最小正周期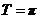 ,因为
,因为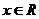 ,
,
所以,当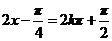 ,即
,即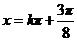 时,
时,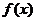 最大值为
最大值为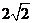 ;
;
(2)证明:欲证明函数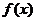 的图像关于直线
的图像关于直线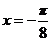 对称,只要证明对任意
对称,只要证明对任意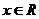 ,有
,有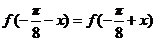 成立,
成立,
因为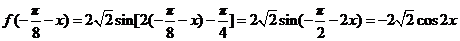 ,
,
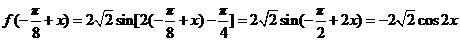 ,
,
所以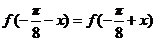 成立,从而函数
成立,从而函数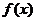 的图像关于直线
的图像关于直线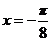 对称。
对称。
例4.
已知函数y=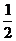 cos2x+
cos2x+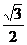 sinx·cosx+1 (x∈R),
sinx·cosx+1 (x∈R),
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图像可由y=sinx(x∈R)的图像经过怎样的平移和伸缩变换得到?
解:(1)y=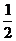 cos2x+
cos2x+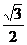 sinx·cosx+1=
sinx·cosx+1=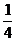 (2cos2x-1)+
(2cos2x-1)+ 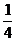 +
+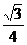 (2sinx·cosx)+1
(2sinx·cosx)+1
=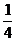 cos2x+
cos2x+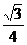 sin2x+
sin2x+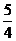 =
=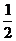 (cos2x·sin
(cos2x·sin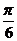 +sin2x·cos
+sin2x·cos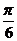 )+
)+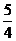
=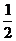 sin(2x+
sin(2x+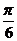 )+
)+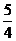
所以y取最大值时,只需2x+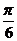 =
=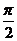 +2kπ,(k∈Z),即
x=
+2kπ,(k∈Z),即
x=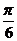 +kπ,(k∈Z)。
+kπ,(k∈Z)。
所以当函数y取最大值时,自变量x的集合为{x|x=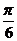 +kπ,k∈Z}
+kπ,k∈Z}
(2)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图像向左平移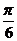 ,得到函数y=sin(x+
,得到函数y=sin(x+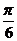 )的图像;
)的图像;
(ii)把得到的图像上各点横坐标缩短到原来的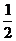 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+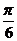 )的图像;
)的图像;
(iii)把得到的图像上各点纵坐标缩短到原来的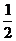 倍(横坐标不变),得到函数y=
倍(横坐标不变),得到函数y=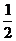 sin(2x+
sin(2x+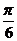 )的图像;
)的图像;
(iv)把得到的图像向上平移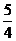 个单位长度,得到函数y=
个单位长度,得到函数y=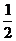 sin(2x+
sin(2x+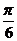 )+
)+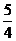 的图像。
的图像。
综上得到y=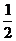 cos2x+
cos2x+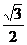 sinxcosx+1的图像。
sinxcosx+1的图像。
说明:本题是2000年全国高考试题,属中档偏容易题,主要考查三角函数的图像和性质。这类题一般有两种解法:一是化成关于sinx,cosx的齐次式,降幂后最终化成y=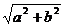 sin (ωx+
sin (ωx+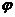 )+k的形式,二是化成某一个三角函数的二次三项式。本题(1)还可以解法如下:当cosx=0时,y=1;当cosx≠0时,y=
)+k的形式,二是化成某一个三角函数的二次三项式。本题(1)还可以解法如下:当cosx=0时,y=1;当cosx≠0时,y=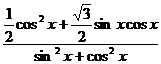 +1=
+1=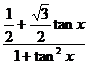 +1
+1
化简得:2(y-1)tan2x-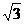 tanx+2y-3=0
tanx+2y-3=0
∵tanx∈R,∴△=3-8(y-1)(2y-3) ≥0,解之得: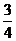 ≤y≤
≤y≤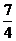
∴ymax=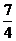 ,此时对应自变量x的值集为{x|x=kπ+
,此时对应自变量x的值集为{x|x=kπ+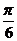 ,k∈Z}
,k∈Z}
例5.已知函数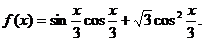
(Ⅰ)将f(x)写成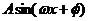 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
解: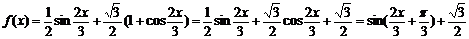
(Ⅰ)由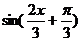 =0即
=0即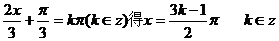
即对称中心的横坐标为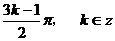
(Ⅱ)由已知b2=ac
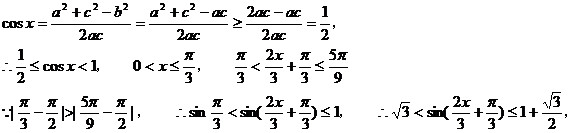 即
即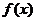 的值域为
的值域为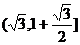 .
.
综上所述,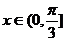 ,
,
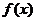 值域为
值域为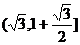 .
.
说明:本题综合运用了三角函数、余弦定理、基本不等式等知识,还需要利用数形结合的思想来解决函数值域的问题,有利于培养学生的运算能力,对知识进行整合的能力。
例6.在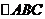 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且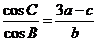 ,
,
(1)求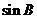 的值;
的值;
(2)若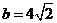 ,且a=c,求
,且a=c,求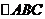 的面积。
的面积。
解:(1)由正弦定理及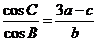 ,有
,有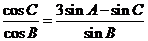 ,
,
即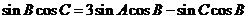 ,所以
,所以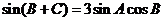 ,
,
又因为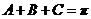 ,
,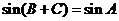 ,所以
,所以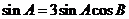 ,因为
,因为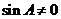 ,所以
,所以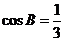 ,又
,又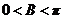 ,所以
,所以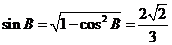 。
。
(2)在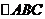 中,由余弦定理可得
中,由余弦定理可得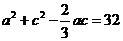 ,又
,又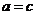 ,
,
所以有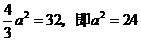 ,所以
,所以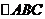 的面积为
的面积为
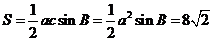 。
。
例7.已知向量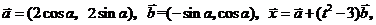
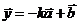 ,且
,且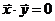 ,
,
(1)求函数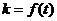 的表达式;
的表达式;
(2)若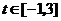 ,求
,求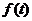 的最大值与最小值。
的最大值与最小值。
解:(1)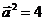 ,
,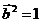 ,
,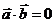 ,又
,又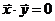 ,
,
所以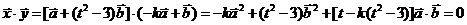 ,
,
所以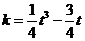 ,即
,即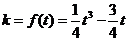 ;
;
(2)由(1)可得,令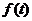 导数
导数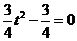 ,解得
,解得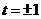 ,列表如下:
,列表如下:
|
t |
-1 |
(-1,1) |
1 |
(1,3) |
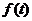 导数 导数 |
0 |
- |
0 |
+ |
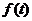 |
极大值 |
递减 |
极小值 |
递增 |
而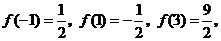 所以
所以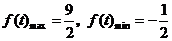 。
。
例8.已知向量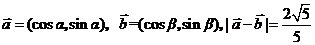 ,
,
(1) 求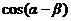 的值;
的值;
(2) (2)若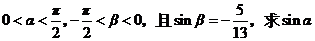 的值。
的值。
解:(1)因为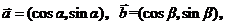
所以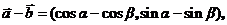
又因为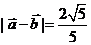 ,所以
,所以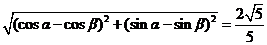 ,
,
即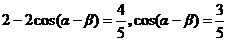 ;
;
(2) 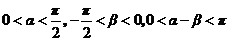 ,
,
又因为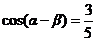 ,所以
,所以 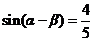 ,
,
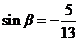 ,所以
,所以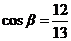 ,所以
,所以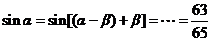
例9.平面直角坐标系有点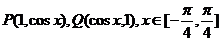
(1)
求向量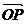 和
和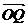 的夹角
的夹角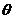 的余弦用
的余弦用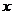 表示的函数
表示的函数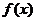 ;
;
(2)
求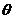 的最值.
的最值.
解:(1)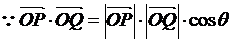 ,
,
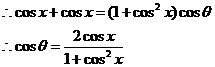
即 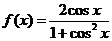
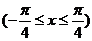
(2)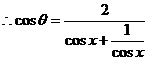 , 又
, 又 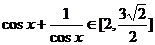 ,
,
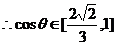 ,
, 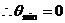 ,
,  .
.
说明:三角函数与向量之间的联系很紧密,解题时要时刻注意。
4.解答三角高考题的策略。
(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com