
题目列表(包括答案和解析)
20、(本题满分12分)
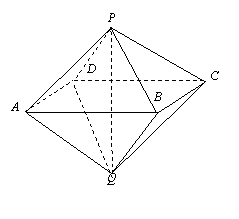
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
⑴ 证明PQ⊥平面ABCD;
⑵ 求异面直线AQ与PB所成的角;
⑶ 求点P到平面QAD的距离.
19、已知数列{log2(an−1)} n∈N *为等差数列,且a1=3, a3=9
(I)求an (II)求证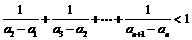
18、(本题满分12分)
一个口袋内装有大小相同且已编有不同号码的6个黑球和4个红球,某人一次从中摸出
2个球
(I)如果摸到的球中含有红球就中奖,那么此人中奖的概率是多少?
(II)如果摸到的2个球都是红球,那么就中大奖,在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
17、 (本题满分12分)
在△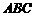 中,已知a、b、
中,已知a、b、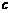 分别是三内角
分别是三内角 、
、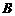 、
、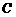 所对应的边长,且
所对应的边长,且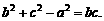
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若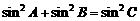 ,求角
,求角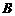 的大小.
的大小.
16、下表给出了四组命题:
|
|
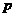 |
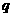 |
|
① |
直线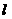 ∥平面 ∥平面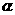 |
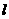 上两点到 上两点到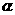 的距离相等 的距离相等 |
|
② |
直线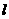 ⊥平面 ⊥平面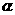 |
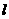 垂直于 垂直于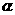 内无数条直线 内无数条直线 |
|
③ |
平面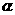 ∥平面 ∥平面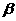 |
直线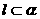 ,且 ,且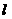 ∥ ∥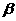 |
|
④ |
平面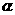 内任一直线平行于平面 内任一直线平行于平面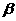 |
平面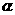 ∥平面 ∥平面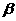 |
其中满足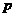 是
是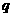 的充分必要条件的序号是_________________。
的充分必要条件的序号是_________________。
15、已知: 命题p:不等式|x-m|+|x-1|>1的解集为R,
命题q:f(x)=log(3+m)x是(0,+∞)上的增函数.
若“p且q”是假命题,“p或q”是真命题,则实数m的取值范围是 .
14.已知函数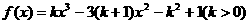 ,若
,若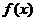 的单调减区间是
的单调减区间是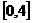 ,则在曲线
,则在曲线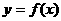 的切线中,斜率最小的切线方程是_________________.
的切线中,斜率最小的切线方程是_________________.
13、在(1-)15的展开式中,系数最大的项是第 项.
12.设对任意实数x∈[−1, 1],不等式x2+ax−3a<0总成立,则实数a的取值范围是
A.a>0 B.a>0或a<−12 C.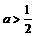 D.
D.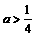
第Ⅱ卷(非选择题 共90分)
11.{an}为等差数列,若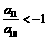 ,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n=
,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n=
A.11 B.17 C.19 D.21
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com