
题目列表(包括答案和解析)
11.设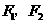 分别是双曲线
分别是双曲线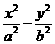 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点 ,使
,使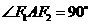 且
且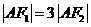 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.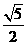 B.
B.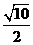 C.
C.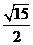 D.
D.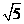
22.(本小题满分14分)
解:(Ⅰ)设椭圆的半焦距为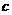 ,依题意
,依题意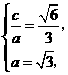
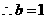 ,
, 所求椭圆方程为
所求椭圆方程为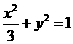 .
.
(Ⅱ)设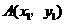 ,
,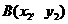 .
.
(1)当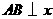 轴时,
轴时,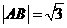 .
.
(2)当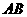 与
与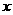 轴不垂直时,
轴不垂直时,
设直线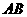 的方程为
的方程为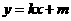 .
.
由已知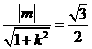 ,得
,得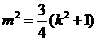 .
.
把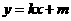 代入椭圆方程,整理得
代入椭圆方程,整理得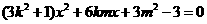 ,
,
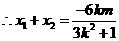 ,
,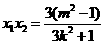 .
.
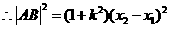
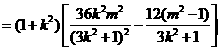
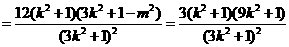
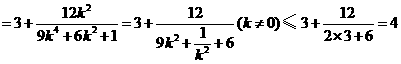 .
.
当且仅当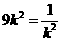 ,即
,即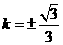 时等号成立.当
时等号成立.当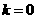 时,
时,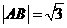 ,
,
综上所述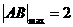 .
.
 当
当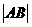 最大时,
最大时, 面积取最大值
面积取最大值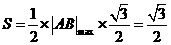 .
.
山东理
(13)设 是坐标原点,
是坐标原点,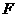 是抛物线
是抛物线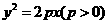 的焦点,
的焦点, 是抛物线上的一点,
是抛物线上的一点,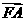 与
与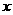 轴正向的夹角为
轴正向的夹角为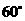 ,则
,则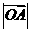 为
.
为
.
(21)(本小题满分12分)
已知椭圆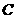 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在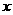 轴上,椭圆
轴上,椭圆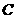 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为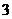 ,最小值为
,最小值为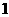 .
.
(Ⅰ)求椭圆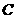 的标准方程;
的标准方程;
(Ⅱ)若直线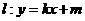 与椭圆
与椭圆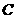 相交于
相交于 ,
,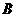 两点(
两点(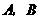 不是左右顶点),且以
不是左右顶点),且以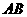 为直径的圆过椭圆
为直径的圆过椭圆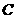 的右顶点,求证:直线
的右顶点,求证:直线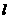 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
[标准答案](I)由题意设椭圆的标准方程为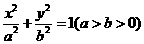
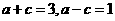 ,
,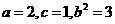
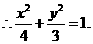
(II)设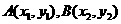 ,由
,由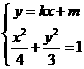 得
得
 ,
,
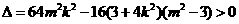 ,
,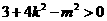 .
.
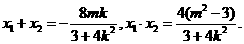
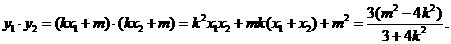
 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点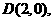
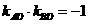 ,
,
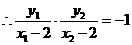 ,
,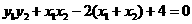 ,
,
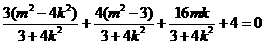 ,
,
 ,解得
,解得
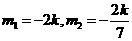 ,且满足
,且满足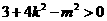 .
.
当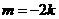 时,
时,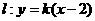 ,直线过定点
,直线过定点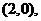 与已知矛盾;
与已知矛盾;
当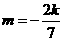 时,
时,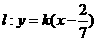 ,直线过定点
,直线过定点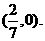
综上可知,直线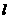 过定点,定点坐标为
过定点,定点坐标为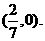
全国2理
22. (本小题满分14分)
已知椭圆C: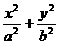 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为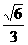 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为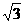 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为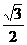 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
9.已知双曲线C∶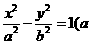 >0,b>0),以C的右焦点为圆心且与C的渐近线相切的圆的半径是
>0,b>0),以C的右焦点为圆心且与C的渐近线相切的圆的半径是
(A)a (B)b (C)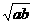 (D)
(D)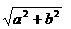
3.抛物线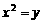 的准线方程是
的准线方程是
(A)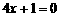 (B)
(B)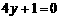
(C)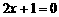 (D)
(D)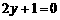
21.解:(1)
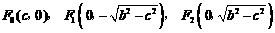 ,
,
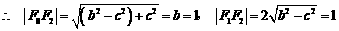 ,
,
于是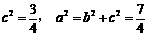 ,
,
所求“果圆”方程为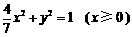 ,
,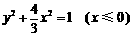 .
.
(2)设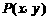 ,则
,则
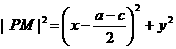
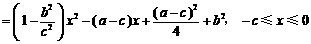 ,
,
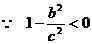 ,
,
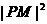 的最小值只能在
的最小值只能在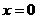 或
或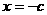 处取到.
处取到.
即当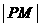 取得最小值时,
取得最小值时,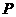 在点
在点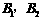 或
或 处.
处.
(3)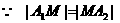 ,且
,且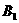 和
和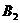 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆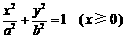 和半椭圆
和半椭圆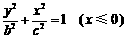 上,所以,由(2)知,只需研究
上,所以,由(2)知,只需研究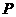 位于“果圆”的半椭圆
位于“果圆”的半椭圆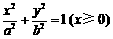 上的情形即可.
上的情形即可.
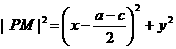
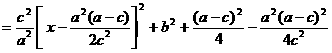 .
.
当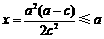 ,即
,即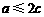 时,
时,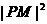 的最小值在
的最小值在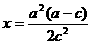 时取到,
时取到,
此时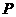 的横坐标是
的横坐标是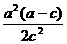 .
.
当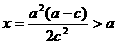 ,即
,即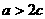 时,由于
时,由于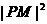 在
在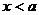 时是递减的,
时是递减的,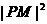 的最小值在
的最小值在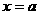 时取到,此时
时取到,此时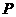 的横坐标是
的横坐标是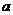 .
.
综上所述,若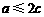 ,当
,当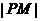 取得最小值时,点
取得最小值时,点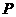 的横坐标是
的横坐标是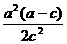 ;若
;若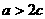 ,当
,当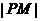 取得最小值时,点
取得最小值时,点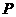 的横坐标是
的横坐标是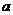 或
或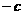 .
.
陕西文
21.[解]
(1)∵F0(c,0)F1(0,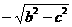 ),F2(0,
),F2(0,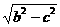 )
)
∴| F0F1 |=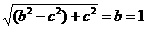 ,| F1F2
|=
,| F1F2
|=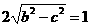
于是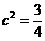 ,
,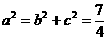 ,所求“果圆”方程为
,所求“果圆”方程为
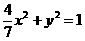 (x≥0),
(x≥0),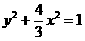 (x≤0). ……4分
(x≤0). ……4分
(2)由题意,得a+c>2b,即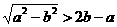 .
.
∵(2b)2>b2+c2,∴a2-b2>(2b-a)2,得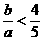 ……7分
……7分
又b2>c2=a2-b2,∴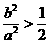 .
.
∴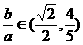 .
.
(3)设“果圆”的方程为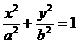 (x≥0)
(x≥0)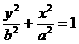 (x≤0)
(x≤0)
记平行弦的斜率为k.
当k=0时,直线y=t(-b≤t≤b)与半椭圆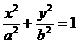 (x≥0)的交点是
(x≥0)的交点是
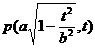 ,与半椭圆
,与半椭圆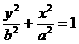 (x≤0)的交点是Q(
(x≤0)的交点是Q(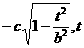 ).
).
∴P、Q的中点M(x,y)满足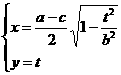
得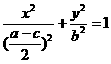 .
.
∵a<2b,∴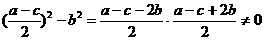 .
.
综上所述,当k=0时,“果圆”平行弦的中点轨迹总是落在某个椭圆……14分
当k>0时,以k为斜率过B1的直线l与半椭圆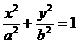 (x≥0)的交点是
(x≥0)的交点是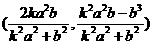
由此,在直线l右测,以k为斜率的平行弦的中点轨迹在直线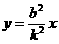 上,即不在某一椭圆上. ……17分
上,即不在某一椭圆上. ……17分
当k<0时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上. ……18分
上海文
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分9分.
我们把由半椭圆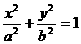
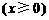 与半椭圆
与半椭圆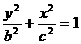
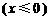 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中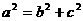 ,
,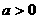 ,
,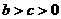 .
.
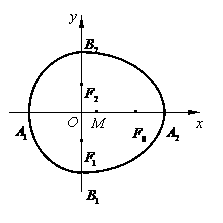 如图,设点
如图,设点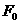 ,
,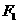 ,
,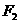 是相应椭圆的焦点,
是相应椭圆的焦点, ,
,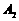 和
和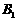 ,
,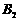 是“果圆” 与
是“果圆” 与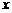 ,
,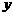 轴的交点,
轴的交点,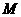 是线段
是线段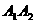 的中点.
的中点.
(1)若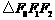 是边长为1的等边三角形,求该
是边长为1的等边三角形,求该
“果圆”的方程;
(2)设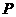 是“果圆”的半椭圆
是“果圆”的半椭圆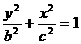
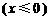 上任意一点.求证:当
上任意一点.求证:当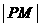 取得最小值时,
取得最小值时,
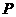 在点
在点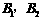 或
或 处;
处;
(3)若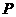 是“果圆”上任意一点,求
是“果圆”上任意一点,求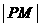 取得最小值时点
取得最小值时点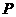 的横坐标.
的横坐标.
21、已知半椭圆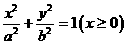 与半椭圆
与半椭圆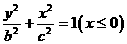 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中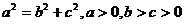 ,
,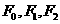 是对应的焦点。
是对应的焦点。
(1)若三角形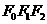 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;
(2)若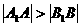 ,求
,求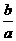 的取值范围;
的取值范围;
(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数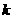 ,使得斜率为
,使得斜率为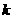 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有
的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有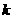 的值;若不存在,说明理由。
的值;若不存在,说明理由。
8、已知双曲线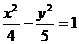 ,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为
,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为
22.本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.
(Ⅰ)证法一:由题设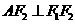 及
及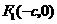 ,
,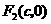 ,不妨设点
,不妨设点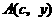 ,其中
,其中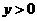 .由于点
.由于点 在椭圆上,有
在椭圆上,有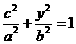 ,即
,即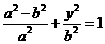 .
.
解得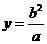 ,从而得到
,从而得到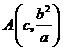 .
.
直线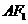 的方程为
的方程为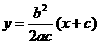 ,整理得
,整理得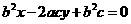 .
.
由题设,原点 到直线
到直线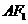 的距离为
的距离为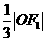 ,即
,即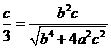 ,
,
将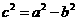 代入上式并化简得
代入上式并化简得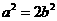 ,即
,即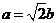 .
.
证法二:同证法一,得到点 的坐标为
的坐标为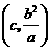 .
.
过点 作
作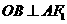 ,垂足为
,垂足为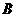 ,易知
,易知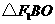
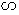
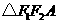 ,故
,故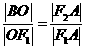 .
.
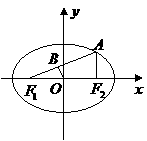 由椭圆定义得
由椭圆定义得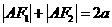 ,又
,又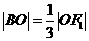 ,
,
所以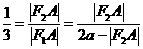 ,
,
解得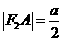 ,而
,而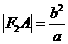 ,得
,得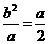 ,即
,即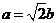 .
.
(Ⅱ)解法一:设点 的坐标为
的坐标为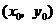 .
.
当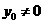 时,由
时,由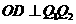 知,直线
知,直线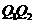 的斜率为
的斜率为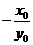 ,所以直线
,所以直线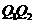 的方程为
的方程为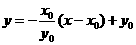 ,或
,或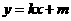 ,其中
,其中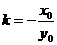 ,
,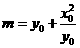 .
.
点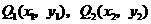 的坐标满足方程组
的坐标满足方程组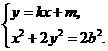
将①式代入②式,得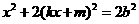 ,
,
整理得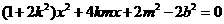 ,
,
于是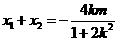 ,
,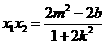 .
.
由①式得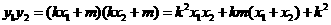
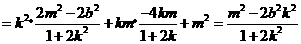 .
.
由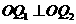 知
知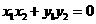 .将③式和④式代入得
.将③式和④式代入得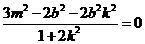 ,
,
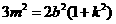 .
.
将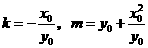 代入上式,整理得
代入上式,整理得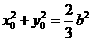 .
.
当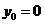 时,直线
时,直线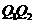 的方程为
的方程为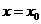 ,
,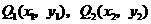 的坐标满足方程组
的坐标满足方程组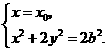
所以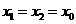 ,
,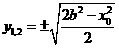 .
.
由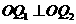 知
知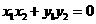 ,即
,即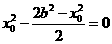 ,
,
解得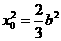 .
.
这时,点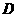 的坐标仍满足
的坐标仍满足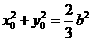 .
.
综上,点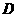 的轨迹方程为
的轨迹方程为 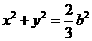 .
.
解法二:设点 的坐标为
的坐标为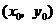 ,直线
,直线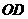 的方程为
的方程为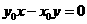 ,由
,由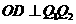 ,垂足为
,垂足为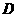 ,可知直线
,可知直线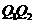 的方程为
的方程为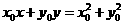 .
.
记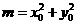 (显然
(显然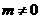 ),点
),点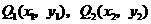 的坐标满足方程组
的坐标满足方程组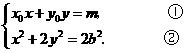
由①式得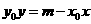 . ③
. ③
由②式得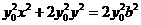 . ④
. ④
将③式代入④式得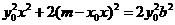 .
.
整理得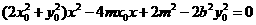 ,
,
于是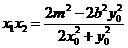 . ⑤
. ⑤
由①式得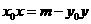 . ⑥
. ⑥
由②式得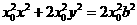 . ⑦
. ⑦
将⑥式代入⑦式得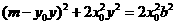 ,
,
整理得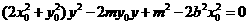 ,
,
于是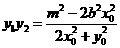 . ⑧
. ⑧
由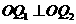 知
知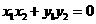 .将⑤式和⑧式代入得
.将⑤式和⑧式代入得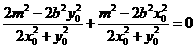 ,
,
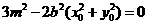 .
.
将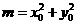 代入上式,得
代入上式,得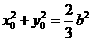 .
.
所以,点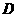 的轨迹方程为
的轨迹方程为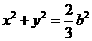 .
.
四川文
(5)如果双曲线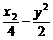 =1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
=1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
(A)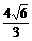 (B)
(B)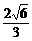 (C)
(C)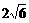 (D)
(D)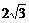
(10)已知抛物线y-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于
A.3
B.4
C.3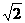 D.4
D.4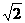
解析:选C.设直线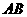 的方程为
的方程为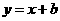 ,由
,由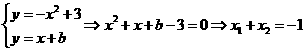 ,进而可求出
,进而可求出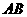 的中点
的中点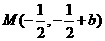 ,又由
,又由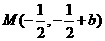 在直线
在直线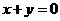 上可求出
上可求出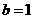 ,∴
,∴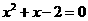 ,由弦长公式可求出
,由弦长公式可求出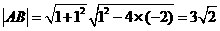 .本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.
.本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.
(21)(本小题满分12分)
求F1、F2分别是椭圆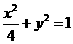 的左、右焦点.
的左、右焦点.
(Ⅰ)若r是第一象限内该数轴上的一点,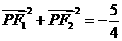 ,求点P的作标;
,求点P的作标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠ADB为锐角(其中O为作标原点),求直线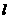 的斜率
的斜率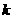 的取值范围.
的取值范围.
解析:本题主要考查直线、椭圆、平面向量的数量积等基础知识,以及综合运用数学知识解决问题及推理计算能力.
(Ⅰ)易知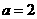 ,
,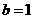 ,
,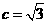 .
.
∴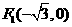 ,
,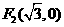 .设
.设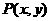
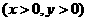 .则
.则
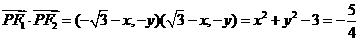 ,又
,又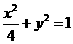 ,
,
联立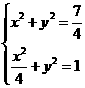 ,解得
,解得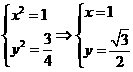 ,
,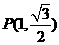 .
.
(Ⅱ)显然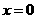 不满足题设条件.可设
不满足题设条件.可设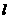 的方程为
的方程为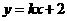 ,设
,设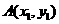 ,
,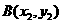 .
.
联立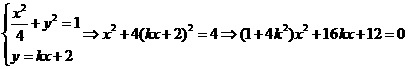
∴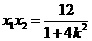 ,
,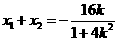
由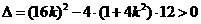
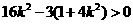 ,
,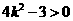 ,得
,得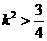 .①
.①
又 为锐角
为锐角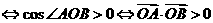 ,
,
∴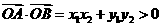
又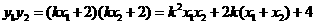
∴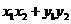
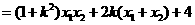
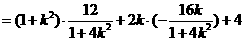
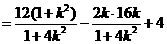
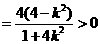
∴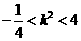 .②
.②
综①②可知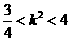 ,∴
,∴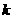 的取值范围是
的取值范围是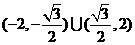 .
.
四川理
20)(本小题满分12分)设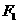 、
、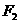 分别是椭圆
分别是椭圆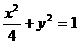 的左、右焦点.
的左、右焦点.
(Ⅰ)若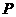 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求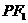 ·
·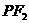 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点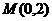 的直线
的直线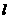 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、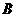 ,且∠
,且∠ 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线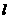 的斜率
的斜率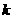 的取值范围.
的取值范围.
(20)本题主要考察直线、椭圆、平面向量的数量积等基础知识,以及综合应用数学知识解决问题及推理计算能力。
解:(Ⅰ)解法一:易知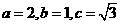
所以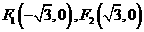 ,设
,设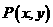 ,则
,则
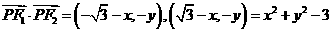
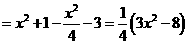
因为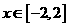 ,故当
,故当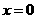 ,即点
,即点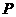 为椭圆短轴端点时,
为椭圆短轴端点时,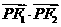 有最小值
有最小值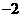
当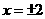 ,即点
,即点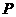 为椭圆长轴端点时,
为椭圆长轴端点时,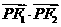 有最大值
有最大值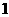
解法二:易知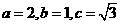 ,所以
,所以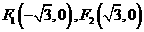 ,设
,设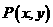 ,则
,则
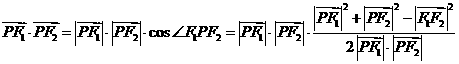
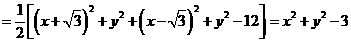 (以下同解法一)
(以下同解法一)
(Ⅱ)显然直线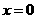 不满足题设条件,可设直线
不满足题设条件,可设直线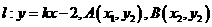 ,
,
联立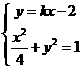 ,消去
,消去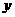 ,整理得:
,整理得: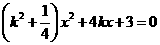
∴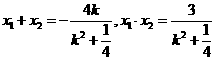
由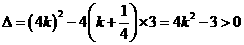 得:
得: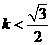 或
或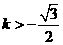
又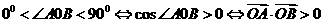
∴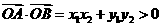
又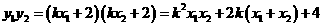
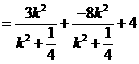
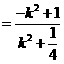
∵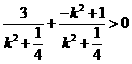 ,即
,即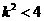 ∴
∴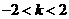
故由①、②得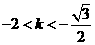 或
或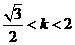
上海理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com