
题目列表(包括答案和解析)
(1)“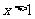 ”是“
”是“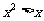 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分不必要条件 D.既不充分也不必要条件
(2)若函数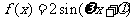 ,
,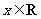 (其中
(其中 ,
,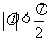 )的最小正周期是
)的最小正周期是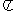 ,且
,且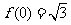 ,则( )
,则( )
A.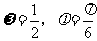 B.
B.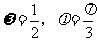
C.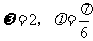 D.
D.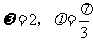
(3)直线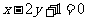 关于直线
关于直线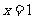 对称的直线方程是( )
对称的直线方程是( )
A.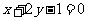 B.
B.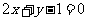
C.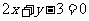 D.
D.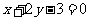
 (4)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需安装这种喷水龙头的个数最少是( )
(4)要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需安装这种喷水龙头的个数最少是( )
A.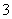 B.
B.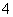 C.
C.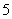 D.
D.
(5)已知随机变量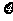 服从正态分布
服从正态分布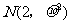 ,
,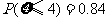 ,则
,则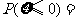 ( )
( )
A.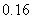 B.
B.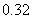 C.
C.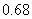 D,
D,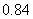
(6)若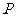 两条异面直线
两条异面直线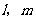 外的任意一点,则( )
外的任意一点,则( )
A.过点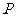 有且仅有一条直线与
有且仅有一条直线与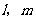 都平行
都平行
B.过点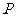 有且仅有一条直线与
有且仅有一条直线与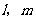 都垂直
都垂直
C.过点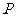 有且仅有一条直线与
有且仅有一条直线与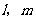 都相交
都相交
D.过点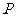 有且仅有一条直线与
有且仅有一条直线与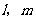 都异面
都异面
(7)若非零向量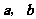 满足
满足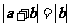 ,则( )
,则( )
A.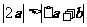 B.
B.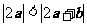
C.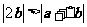 D.
D. 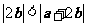
(8)设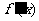 是函数
是函数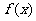 的导函数,将
的导函数,将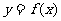 和
和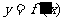 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )
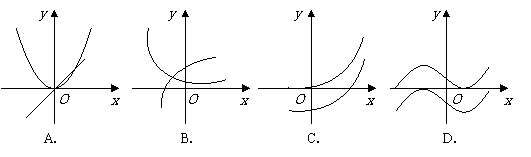
(9)已知双曲线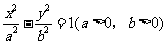 的左、右焦点分别为
的左、右焦点分别为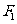 ,
,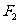 ,
,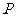 是准线上一点,且
是准线上一点,且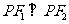 ,
,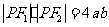 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.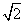 B.
B.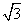 C.
C.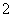 D.
D.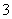
(10)设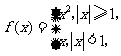
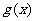 是二次函数,若
是二次函数,若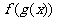 的值域是
的值域是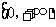 ,则
,则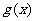 的值域是( )
的值域是( )
A.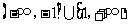 B.
B.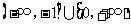
C.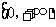 D.
D.
第II卷(共100分)
22.(本小题满分14分)
已知椭圆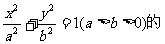 一个顶点为A(0,1),且它的离心率与双曲线
一个顶点为A(0,1),且它的离心率与双曲线
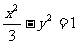 的离心率互为倒数.
的离心率互为倒数.
(I)求椭圆的方程;
(Ⅱ)过A点且斜率为k的直线与椭圆相交于A、B两点,点M在椭圆上,并且满足
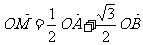 ,求k的值.
,求k的值.
21.(本小题满分12分)
已知数列{an}满足a1=1,a2=-13,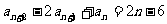
(Ⅰ)设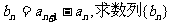 的通项公式;
的通项公式;
(Ⅱ)求n为何值时,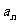 最小(不需要求
最小(不需要求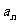 的最小值)
的最小值)
20.(本小题满分12分)
某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(Ⅰ)设该厂每x天购买一次原材料,试写出每次购买的原材料在x天内总的保管费用y1关于关于x的函数关系式;
(Ⅱ)求该厂多少天购买一次原材料才能使平均每天支付的总费用y最少,并求出这个最少(小)值;
19.(本小题满分12分)
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为BD、BB1的中点,
(Ⅰ)求证:EF⊥AD1;
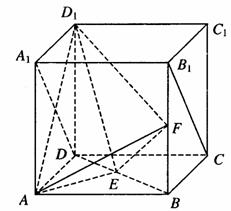 (Ⅱ)求二面角E-D1F-A的大小;
(Ⅱ)求二面角E-D1F-A的大小;
(Ⅲ)求三棱锥D1-AEF的体积.
18.(本小题满分12分)
已知函数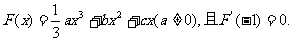
(Ⅰ)若F(x)在x=1处取得极小值-2,求函数F(x)的单调区间;
(Ⅱ)令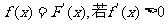 的解集为A,且满足A∪(0,1)=(0,+∞),求
的解集为A,且满足A∪(0,1)=(0,+∞),求
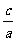 的取值范围.
的取值范围.
17.(本小题满分12分)
已知向量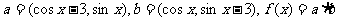
(Ⅰ)若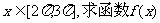 的单调增区间;
的单调增区间;
|
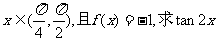 的值.
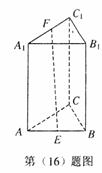
的值.16.如图,正三棱柱ABC-A1B1C1的底边长为2,
侧棱长为4,E、F分别是AB、A1C1的中点,
则EF的长等于 .
15.双曲线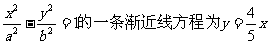 ,
,
则双曲线的离心率为 .
13.数据5,7,7,8,10,11的标准差是 .
 14.从含有两件正品a1,a2和一件次品b1的3件产品中每次任取1件,每次取出后不放回,连续取两次,则取出的两件产品中恰有一件次品的概率是
.
14.从含有两件正品a1,a2和一件次品b1的3件产品中每次任取1件,每次取出后不放回,连续取两次,则取出的两件产品中恰有一件次品的概率是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com