
题目列表(包括答案和解析)
3.某校高一高二年级各有300人,高三年级有400人,现采用分层抽样抽取容量为50人的
样本,那么高三年级应抽人数为 ( )
A.16 B.40 C.20 D.25
2.已知集合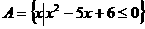 ,
,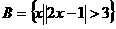 ,则集合
,则集合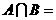 ( )
( )
A.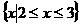 B.
B.
C.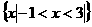 D.
D.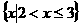
1.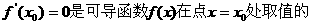 ( )
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
19.本小题主要考查排列、组合知识与等可能事件、互斥事件概率的计算,运用概率知识分析问题及解决实际问题的能力.本小题满分13分.
解:以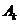 表示恰剩下
表示恰剩下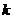 只果蝇的事件
只果蝇的事件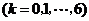 .
.
以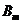 表示至少剩下
表示至少剩下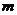 只果蝇的事件
只果蝇的事件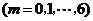 .
.
可以有多种不同的计算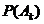 的方法.
的方法.
方法1(组合模式):当事件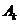 发生时,第
发生时,第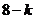 只飞出的蝇子是苍蝇,且在前
只飞出的蝇子是苍蝇,且在前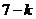 只飞出的蝇子中有1只是苍蝇,所以
只飞出的蝇子中有1只是苍蝇,所以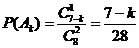 .
.
方法2(排列模式):当事件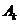 发生时,共飞走
发生时,共飞走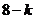 只蝇子,其中第
只蝇子,其中第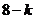 只飞出的蝇子是苍蝇,哪一只?有两种不同可能.在前
只飞出的蝇子是苍蝇,哪一只?有两种不同可能.在前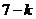 只飞出的蝇子中有
只飞出的蝇子中有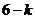 只是果蝇,有
只是果蝇,有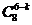 种不同的选择可能,还需考虑这
种不同的选择可能,还需考虑这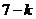 只蝇子的排列顺序.所以
只蝇子的排列顺序.所以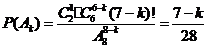 .
.
由上式立得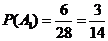 ;
;
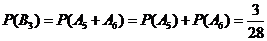 .
.
20.本小题主要考查等可能场合下的事件概率的计算、离散型随机变量的分布列、数学期望的概念及其计算,考查分析问题及解决实际问题的能力.本小题满分13分.
解:(Ⅰ) 的分布列为:
的分布列为:
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
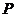 |
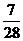 |
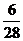 |
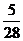 |
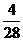 |
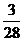 |
 |
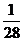 |
(Ⅱ)数学期望为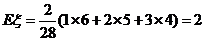 .
.
(Ⅲ)所求的概率为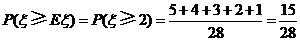 .
.
安徽文
(19)(本小题满分13分)
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率;
(Ⅱ)求笼内至少剩下5只果蝇的概率.
18.(共13分)
解:(I)这6位乘客在互不相同的车站下车的概率为
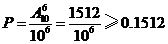 .
.
(II)这6位乘客中恰有3人在终点站下车的概率为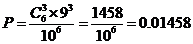 .
.
安徽理
(10)以 表示标准正态总体在区间(
表示标准正态总体在区间( )内取值的概率,若随机变量
)内取值的概率,若随机变量 服从正态分布
服从正态分布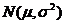 ,则概率
,则概率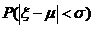 等于
等于
(A) -
-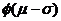 (B)
(B)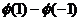
(C)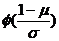 (D)
(D)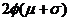
(20) (本小题满分13分)
在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数.
(Ⅰ)写出ξ的分布列(不要求写出计算过程);
(Ⅱ)求数学期望Eξ;
(Ⅲ)求概率P(ξ≥Eξ).
18.(本小题共12分)
某条公共汽车线路沿线共有11个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有6位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
(I)这6位乘客在其不相同的车站下车的概率;
(II)这6位乘客中恰有3人在终点站下车的概率;
18.(共13分)
解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40.
(I)该合唱团学生参加活动的人均次数为 .
.
(II)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为 .
.
(III)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件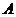 ,“这两人中一人参加2次活动,另一人参加3次活动”为事件
,“这两人中一人参加2次活动,另一人参加3次活动”为事件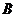 ,“这两人中一人参加1次活动,另一人参加3次活动”为事件
,“这两人中一人参加1次活动,另一人参加3次活动”为事件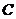 .易知
.易知
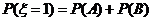
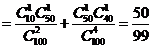 ;
;
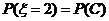
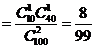 ;
;
 的分布列:
的分布列:
 |
0 |
1 |
2 |
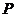 |
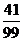 |
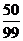 |
 |
 的数学期望:
的数学期望: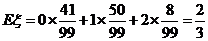 .
.
18.(本小题共13分)
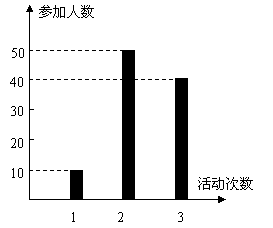 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
18.本小题主要考查概率的基础知识,运用数学知识解决问题的能力,以及推理与运算能力.满分12分.
解:记“甲第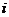 次试跳成功”为事件
次试跳成功”为事件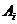 ,“乙第
,“乙第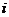 次试跳成功”为事件
次试跳成功”为事件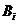 ,依题意得
,依题意得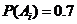 ,
,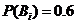 ,且
,且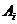 ,
,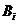 (
(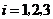 )相互独立.
)相互独立.
(Ⅰ)“甲第三次试跳才成功”为事件 ,且三次试跳相互独立,
,且三次试跳相互独立,
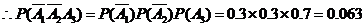 .
.
答:甲第三次试跳才成功的概率为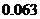 .
.
(Ⅱ)“甲、乙两人在第一次试跳中至少有一人成功”为事件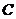 .
.
解法一: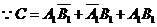 ,且
,且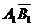 ,
,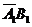 ,
,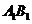 彼此互斥,
彼此互斥,
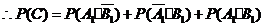
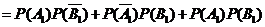
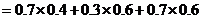
 .
.
解法二: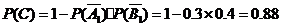 .
.
答:甲、乙两人在第一次试跳中至少有一人成功的概率为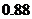 .
.
(Ⅲ)设“甲在两次试跳中成功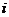 次”为事件
次”为事件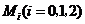 ,
,
“乙在两次试跳中成功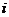 次”为事件
次”为事件 ,
,
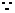 事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为
事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为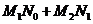 ,且
,且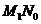 ,
,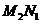 为互斥事件,
为互斥事件,
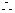 所求的概率为
所求的概率为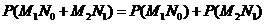

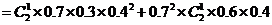
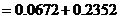
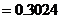
答:甲、乙每人试跳两次,甲比乙的成功次数恰好多一次的概率为 .
.
北京理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com