
题目列表(包括答案和解析)
24.已知函数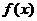 的定义域为
的定义域为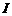 ,导数
,导数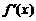 满足0<
满足0<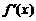 <2
且
<2
且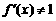 ,常数
,常数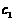 为方程
为方程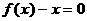 的实数根,常数
的实数根,常数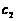 为方程
为方程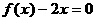 的实数根.
的实数根.
(Ⅰ)若对任意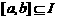 ,存在
,存在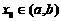 ,使等式
,使等式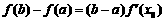 成立.试问:方程
成立.试问:方程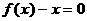 有几个实数根;
有几个实数根;
(Ⅱ)求证:当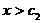 时,总有
时,总有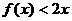 成立;
成立;
(Ⅲ)对任意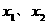 ,若满足
,若满足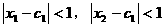 ,求证:
,求证: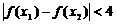 。
。
23.已知O为坐标原点,点E、F的坐标分别为(-1,0)、(1,0),动点A、M、N满足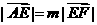 (
(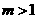 ),
),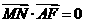 ,
,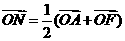 ,
,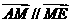 .
.
(Ⅰ)求点M的轨迹W的方程;
(Ⅱ)点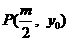 在轨迹W上,直线PF交轨迹W于点Q,且
在轨迹W上,直线PF交轨迹W于点Q,且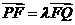 ,若
,若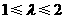 ,求实数
,求实数 的范围.
的范围.
解:(Ⅰ)∵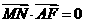 ,
,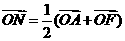 ,
,
∴ MN垂直平分AF.
又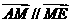 ,∴ 点M在AE上,
,∴ 点M在AE上,
∴ 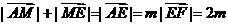 ,
,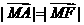 ,
,
∴ 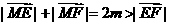 ,
,
∴ 点M的轨迹W是以E、F为焦点的椭圆,且半长轴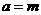 ,半焦距
,半焦距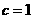 ,
,
∴ 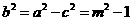 .
.
∴ 点M的轨迹W的方程为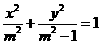 (
(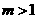 ).
).
(Ⅱ)设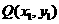
∵ 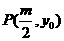 ,
,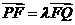 ,
,
∴ 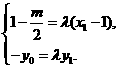 ∴
∴ 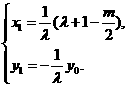
由点P、Q均在椭圆W上,
∴ 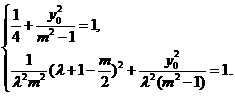
消去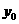 并整理,得
并整理,得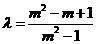 ,
,
由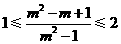 及
及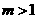 ,解得
,解得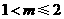 .
.
22.设函数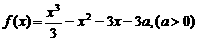 .
.
(Ⅰ)如果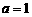 ,点P
,点P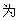 曲线
曲线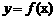 上一个动点,求以P为切点的切线其斜率取最小值时的切线方程;
上一个动点,求以P为切点的切线其斜率取最小值时的切线方程;
(Ⅱ)若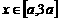 时,
时,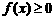 恒成立,求
恒成立,求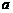 的取值范围.
的取值范围.
.解(Ⅰ)设切线斜率为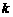 则
则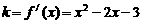 当
当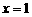 时
时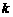 最小值为
最小值为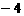 .
.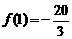
所以切线方程为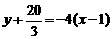 即
即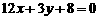
(Ⅱ)由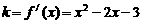 >0
>0 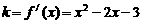 <0得.
<0得.
函数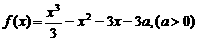 在
在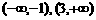 为增函数,在
为增函数,在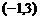 减函数
减函数
(1)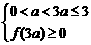 ,无解; (2)
,无解; (2)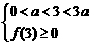 无解;
无解;
(3)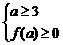 ,解得
,解得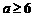 .综上所述
.综上所述 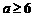 .
.
21.已知函数f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,且f '(1)=0.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设数列{an}满足条件:a1∈(1,2),an+1=f (an)
求证:(a1- a2)·(a3-1)+(a2- a3)·(a4-1)+…+(an- an+1)·(an+2-1)<1
解:(Ⅰ)由f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,所以
x3+ax2+bx+c+(2-x)3+a(2-x)2+b(2-x)+c=2
对一切实数x恒成立.得:a=-3,b+c=3,
对由f '(1)=0,得b=3,c=0,
故所求的表达式为:f(x)= x3-3x2+3x.
(Ⅱ) an+1=f (an)= an 3-3 an 2+3 an (1)
令bn=an-1,0<bn<1,由代入(1)得:bn+1=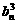 ,bn=
,bn=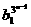 ,
,
∴ 1>bn >bn+1 >0
(a1-a2)·(a3-1)+(a2-a3)·(a4-1)+…+(an-an+1)·(an+2-1)=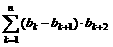
<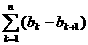 =b1-bn+1<b1<1。
=b1-bn+1<b1<1。
20.已知数列{an}满足a1=1,a2=-13,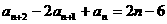
(Ⅰ)设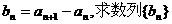 的通项公式;
的通项公式;
(Ⅱ)求n为何值时,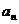 最小(不需要求
最小(不需要求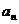 的最小值)
的最小值)
解:(I)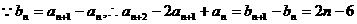
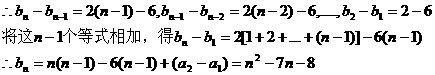
即数列{bn}的通项公式为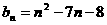
(Ⅱ)若an最小,则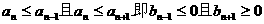
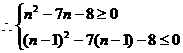 注意n是正整数,解得8≤n≤9
注意n是正整数,解得8≤n≤9
∴当n=8或n=9时,an的值相等并最小
19.定义在N*上的函数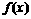 满足:f(0) = 2,f(1) = 3,
满足:f(0) = 2,f(1) = 3,
且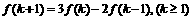 .
.
(Ⅰ)求f(n)(nÎN*);
(Ⅱ)求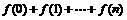 .
.
(Ⅰ)由题意: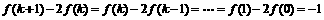 ,所以有:
,所以有: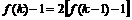 ,又
,又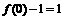 ,所以
,所以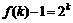 ,即
,即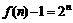 ,故
,故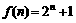 .
.
(Ⅱ)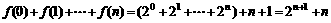 .
.
18.等差数列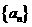 的前
的前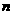 项和为
项和为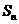 ,公差
,公差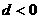 . 若存在正整数
. 若存在正整数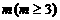 ,使得
,使得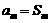 ,则当
,则当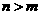 (
(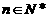 )时,有
)时,有 (填“>”、“<”、“=”).
(填“>”、“<”、“=”).

(6)设等差数列{an}的前n项和为Sn,已知S12>0,S13<0,则 ,,…, 中最大的是 B
(A) (B) (C) (D)
17.已知△ABC,若对任意t∈R,≥,则C
A.∠A=900 B.∠B=900 C.∠C=900 D.∠A=∠B=∠C=600
16.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f (x)的图象恰好通过k个格点,则称函数f (x)为k阶格点函数.下列函数:①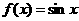 ;②
;②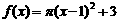 ;③
;③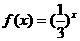 ;④
;④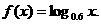 其中是一阶格点函数的有 ①②④ .(填上所有满足题意的序号)
其中是一阶格点函数的有 ①②④ .(填上所有满足题意的序号)
15.已知双曲线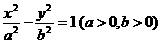 的右焦点为F,右准线与一条渐近线交于点A,
的右焦点为F,右准线与一条渐近线交于点A,
△OAF的面积为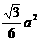 (O为坐标原点),则双曲线的两条渐近线的夹角为 60°
(O为坐标原点),则双曲线的两条渐近线的夹角为 60°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com