
题目列表(包括答案和解析)
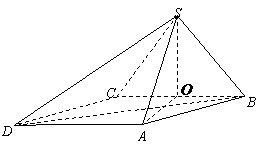
27.(全国Ⅰ•理•19题)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD。已知∠ABC=45°,AB=2,BC=2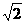 ,SA=SB=
,SA=SB=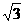 。
。
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小;
解答:解法一:
(Ⅰ)作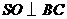 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面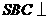 底面
底面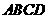 ,得
,得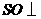 底面
底面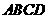 .
.
因为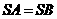 ,所以
,所以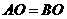 ,
,
又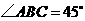 ,故
,故 为等腰直角三角形,
为等腰直角三角形,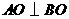 ,
,
由三垂线定理,得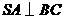 .
.
 (Ⅱ)由(Ⅰ)知
(Ⅱ)由(Ⅰ)知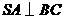 ,依题设
,依题设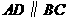 ,
,
故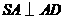 ,由
,由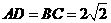 ,
,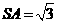 ,
,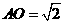 ,得
,得
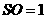 ,
,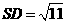 .
.
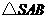 的面积
的面积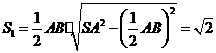 .
.
连结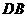 ,得
,得 的面积
的面积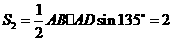
设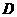 到平面
到平面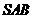 的距离为
的距离为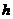 ,由于
,由于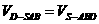 ,得
,得
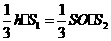 ,
,
解得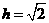 .
.
设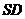 与平面
与平面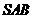 所成角为
所成角为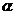 ,则
,则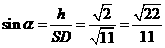 .
.
所以,直线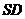 与平面
与平面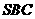 所成的我为
所成的我为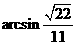 .
.
解法二:
(Ⅰ)作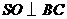 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面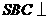 底面
底面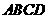 ,得
,得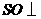 平面
平面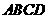 .
.
因为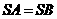 ,所以
,所以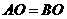 .
.
又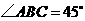 ,
, 为等腰直角三角形,
为等腰直角三角形,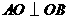 .
.
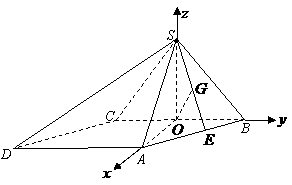 如图,以
如图,以 为坐标原点,
为坐标原点, 为
为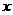 轴正向,建立直角坐标系
轴正向,建立直角坐标系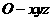 ,
,
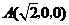 ,
,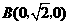 ,
,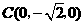 ,
,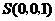 ,
,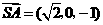 ,
,
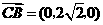 ,
,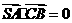 ,所以
,所以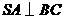 .
.
(Ⅱ)取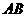 中点
中点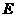 ,
,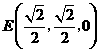 ,
,
连结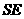 ,取
,取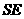 中点
中点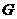 ,连结
,连结 ,
,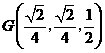 .
.
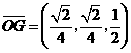 ,
,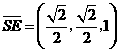 ,
,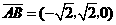 .
.
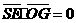 ,
,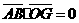 ,
, 与平面
与平面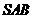 内两条相交直线
内两条相交直线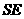 ,
,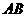 垂直.
垂直.
所以 平面
平面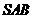 ,
,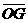 与
与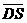 的夹角记为
的夹角记为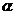 ,
,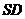 与平面
与平面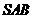 所成的角记为
所成的角记为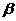 ,则
,则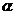 与
与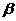 互余.
互余.
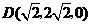 ,
,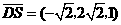 .
.
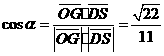 ,
,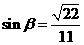 ,
,
所以,直线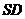 与平面
与平面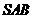 所成的角为
所成的角为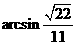 .
.
27.(浙江•理•16题)已知点O在二面角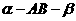 的棱上,点P在
的棱上,点P在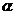 内,且
内,且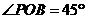 。若对于
。若对于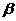 内异于O的任意一点Q,都有
内异于O的任意一点Q,都有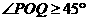 ,则二面角
,则二面角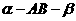 的大小是____
的大小是____ ____。
____。
26.(天津•理•12题)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 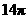 .
.
25.(四川•理•14题)如图,在正三棱柱ABC-A1B1C1中,侧棱长为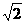 ,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是
,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是 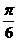 .
.
24. (上海•理•10题)平面内两直线有三种位置关系:相交,平行与重合。已知两个相交平面
(上海•理•10题)平面内两直线有三种位置关系:相交,平行与重合。已知两个相交平面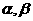 与两直线
与两直线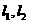 ,又知
,又知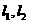 在
在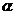 内的射影为
内的射影为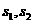 ,在
,在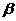 内的射影为
内的射影为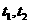 。试写出
。试写出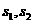 与
与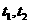 满足的条件,使之一定能成为
满足的条件,使之一定能成为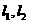 是异面直线的充分条件
是异面直线的充分条件 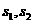 平行,
平行,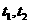 相交 。
相交 。
23.(辽宁•理•15题)若一个底面边长为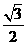 ,棱长为
,棱长为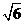 的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
22.(江苏•理•14题)正三棱锥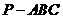 高为2,侧棱与底面所成角为
高为2,侧棱与底面所成角为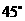 ,则点
,则点 到侧面
到侧面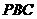 的距离是 .
的距离是 .
21.(安徽•理•15题)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号)。
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体。
20.(全国Ⅱ•理•15题)一个正四棱柱的各个顶点在一个直径为2cm的球面上。如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为
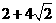 cm2。
cm2。
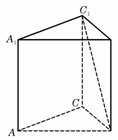
19.(全国Ⅰ•理•16题)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上。已知正三棱柱的底面边长为2,则该三角形的斜边长为 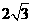 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com