
题目列表(包括答案和解析)
8.(★★★★)一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元.
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
7.(★★★★★)二次函数f(x)=px2+qx+r中实数p、q、r满足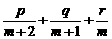 =0,其中m>0,求证:
=0,其中m>0,求证:
(1)pf(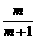 )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
6.(★★★★)如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,试求m的取值范围.
5.(★★★★★)已知实数t满足关系式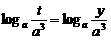 (a>0且a≠1)
(a>0且a≠1)
(1)令t=ax,求y=f(x)的表达式;
(2)若x∈(0,2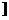 时,y有最小值8,求a和x的值.
时,y有最小值8,求a和x的值.
4.(★★★★★)二次函数f(x)的二次项系数为正,且对任意实数x恒有f(2+x)=f(2-x),若f(1-2x2)<f(1+2x-x2),则x的取值范围是_________.
3.(★★★★★)已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1,若在区间[-1,1]内至少存在一个实数c,使f(c)>0,则实数p的取值范围是_________.
2.(★★★★)设二次函数f(x)=x2-x+a(a>0),若f(m)<0,则f(m-1)的值为( )
A.正数 B.负数
C.非负数 D.正数、负数和零都有可能
1.(★★★★)若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则a的取值范围是( )
A.(-∞,2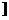 B.
B.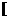 -2,2
-2,2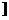 C.(-2,2
C.(-2,2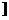 D.(-∞,-2)
D.(-∞,-2)
10.(北师大版第150页B组第6题)三角恒等变换
化简: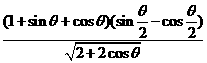 .
.
变式1:函数y=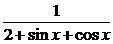 的最大值是( ).
的最大值是( ).
A.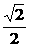 -1 B.
-1 B.
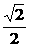 +1 C.1-
+1 C.1-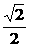 D.-1-
D.-1-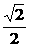
答案选B
变式2:已知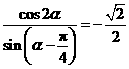 ,求
,求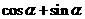 的值.
的值.
解:∵
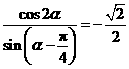 ,
,
∴ 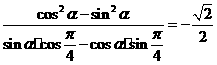
即
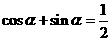 .
.
变式3:已知函数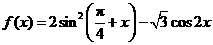 ,
,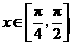 .求
.求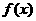 的最大值和最小值.
的最大值和最小值.
解: 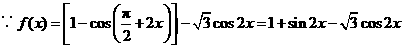
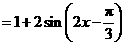 .
.
又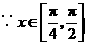 ,
,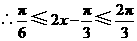 ,即
,即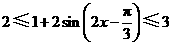 ,
,
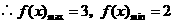 .
.
9.(北师大版第144页A组第1题)三角函数的简单应用
电流I随时间t
变化的关系式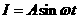 ,
,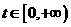 ,设
,设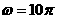
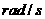 ,
,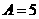 .
.
(1)  求电流I变化的周期;
求电流I变化的周期;
(2)
当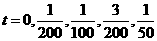 (单位
(单位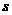 )时,求电流I.
)时,求电流I.
变式1:已知电流I与时间t的关系式为 .
.
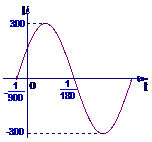
(1)右图是 (ω>0,
(ω>0,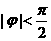 )
)
在一个周期内的图象,根据图中数据求 的解析式;
的解析式;
(2)如果t在任意一段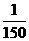 秒的时间内,电流
秒的时间内,电流 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
解:(1)由图可知 A=300.
设t1=-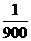 ,t2=
,t2=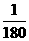 ,
,
则周期T=2(t2-t1)=2(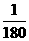 +
+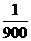 )=
)=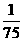 .
.
∴ ω=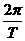 =150π.
=150π.
又当t=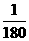 时,I=0,即sin(150π·
时,I=0,即sin(150π·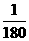 +
+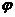 )=0,
)=0,
而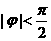 , ∴
, ∴ 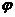 =
=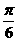 .
.
故所求的解析式为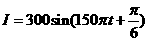 .
.
(2)依题意,周期T≤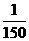 ,即
,即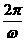 ≤
≤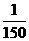 ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943.
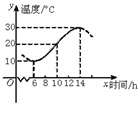 变式2:如图,某地一天从6时至14时的温度变化曲线近似
变式2:如图,某地一天从6时至14时的温度变化曲线近似
满足函数y=Asin(ωx+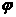 )+b.
)+b.
(Ⅰ)求这段时间的最大温差;
(Ⅱ)写出这段曲线的函数解析式.
解:(1)由题中图所示,这段时间的最大温差是:
30-10=20(℃).
(2)图中从6时到14时的图象是函数y=Asin(ωx+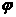 )+b的半个周期的图象,
)+b的半个周期的图象,
∴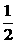 ·
·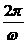 =14-6,解得ω=
=14-6,解得ω=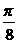 .
.
由图示,A=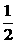 (30-10)=10,b=
(30-10)=10,b=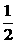 (30+10)=20.
(30+10)=20.
这时y=10sin(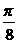 x+
x+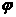 )+20.
)+20.
将x=6,y=10代入上式,可取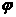 =
=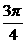 .
.
综上,所求的解析式为y=10sin(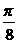 x+
x+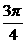 )+20,x∈[6,14]
)+20,x∈[6,14]
 变式3:如图,单摆从某点给一个作用力后开始来回摆动,
变式3:如图,单摆从某点给一个作用力后开始来回摆动,
离开平衡位置O的距离s厘米和时间t秒的函数关系
为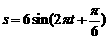 .
.
(1)单摆摆动5秒时,离开平衡位置多少厘米?
(2)单摆摆动时,从最右边到最左边的距离为多少厘米?
(3)单摆来回摆动10次所需的时间为多少秒?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com