
题目列表(包括答案和解析)
7.在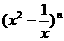 的展开式中,常数项为15项,则n的值为 ( )
的展开式中,常数项为15项,则n的值为 ( )
A.6 B.5 C.4 D.3
6.已知向量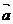 = (-1,2),
= (-1,2),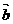 = (2,1),则
= (2,1),则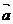 与
与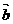 的位置关系是 ( )
的位置关系是 ( )
A.平行且同向 B.不垂直也不平行 C.垂直 D.平行且反向
5.设a1 = 2,数列|1+2an|是以3为公比的等比数列,则a4的值为 ( )
A.67 B.77 C.22 D.202
4.设a.b为两条直线,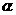 .β为两个平面,则下列命题正确的是 ( )
.β为两个平面,则下列命题正确的是 ( )
A.a.b与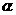 成等角,则a//b;
成等角,则a//b;
B.若a∥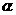 ,b∥β,
,b∥β,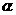 ∥β则
∥β则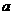 ∥b;
∥b;
C.a 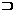
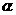 ,b
,b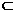 β,a∥b则
β,a∥b则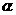 ∥β;
∥β;
D.a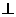
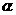 ,b
,b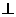 β,
β,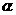 ∥β则
∥β则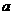 ∥b.
∥b.
3.双曲线中心在原点,实轴长为2,它的一个焦点为抛物线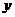 2 = 8
2 = 8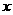 的焦点,则此双曲线方程为 ( )
的焦点,则此双曲线方程为 ( )
A.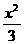 -y2 =
1 B.
-y2 =
1 B.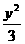 -x2 =
1 C.y2 -
-x2 =
1 C.y2 -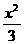 = 1 D.x2 -
= 1 D.x2 -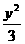 = 1
= 1
2.已知全集U = Z ,A={1,3,5},B={ 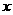 |
| 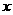 3 - 2
3 - 2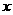 2 - 3
2 - 3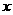 = 0},则B∩CuA等于( )
= 0},则B∩CuA等于( )
A.{1,3} B.{0,-1} C.{1,5} D.{0,1}
1.下列函数中,周期为π,且为偶函数的是 ( )
A.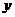 = | sin
= | sin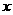 | B.
| B.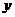 = 2sin
= 2sin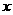 ·cos
·cos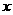
C.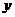 = cos D.
= cos D.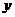 =cos
=cos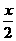
22.(14分)
设函数g(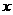 )对任意的
)对任意的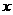 、
、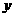 ∈(0,+
∈(0,+ ),都有g(
),都有g(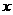 ·
·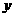 )=g(
)=g(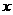 ) + g(
) + g(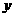 )成立,又g(2) = 1;已知点pn(an,bn)(n ∈ N* )都在直线
)成立,又g(2) = 1;已知点pn(an,bn)(n ∈ N* )都在直线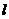 :
: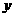 = 2
= 2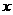 + 2上,P1为直线
+ 2上,P1为直线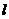 与
与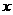 轴的交点,数列{bn}满足n ≥ 2时,bn >0,且g(sn) = g(bn) + g(2+bn) - 2,(n ∈ N* ),其中Sn是数列{bn}的前n项和.
轴的交点,数列{bn}满足n ≥ 2时,bn >0,且g(sn) = g(bn) + g(2+bn) - 2,(n ∈ N* ),其中Sn是数列{bn}的前n项和.
(1)求数列{an}、{bn}的通项公式;
(2)若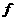 (n) =
(n) =  是否存在
是否存在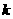 ∈N*,使得
∈N*,使得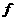 (
(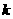 +5)=2
+5)=2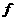 (
(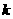 )-2成立?
)-2成立?
若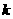 存在,求出
存在,求出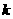 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)求证: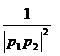 +
+ 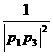 + … +
+ … + 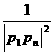 <
< 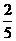 .(n ≥ 2,n ∈ N* )
.(n ≥ 2,n ∈ N* )
21.(12分)设椭圆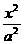 +
+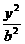 = 1( a > b > 0 )的左焦点为F,上顶点为A.过A做直线
= 1( a > b > 0 )的左焦点为F,上顶点为A.过A做直线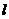
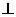 AF
AF
l分别交椭圆和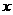 轴正半轴于P、Q两点,若
轴正半轴于P、Q两点,若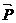 分AQ所成的比为8∶5.
分AQ所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过A、Q、F三点的圆恰好与直线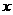 +
+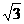
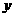 + 3 = 0相切,求椭圆方程.
+ 3 = 0相切,求椭圆方程.
20.(12分)已知函数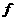 (
(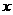 ) = a
) = a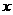 3 + b
3 + b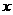 2 + c(a,b,c∈R,a≠0) 的图像过点P( -1, 2 ),且在点P处的切线与直线
2 + c(a,b,c∈R,a≠0) 的图像过点P( -1, 2 ),且在点P处的切线与直线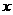 - 3
- 3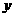 = 0垂直.
= 0垂直.
(1)若c = 0试求函数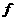 (
(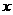 )的单调区间;
)的单调区间;
(2)若 a > 0 , b > 0且 ( - , m ) , ( n ,+
, m ) , ( n ,+ )是
)是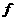 (
(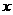 )的单调递增区间,试求n - m的范围.
)的单调递增区间,试求n - m的范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com