
题目列表(包括答案和解析)
16.解:(1)因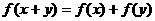 ,
,
令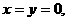 得
得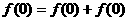 ,即
,即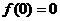 ;………………………1分
;………………………1分
再令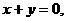 即
即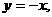 得
得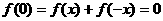 ,
,
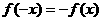 ,
,

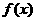 为奇函数……………………………………………3分
为奇函数……………………………………………3分
(2)设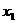 、
、 ,且
,且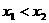 ,
,
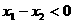 ,由已知得
,由已知得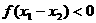 。……4分
。……4分

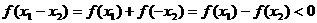 ,………………………6分
,………………………6分

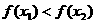

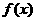 为
为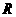 上的增函数;……………………………………7分.
上的增函数;……………………………………7分.
(3)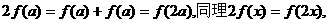 ……………………8分.
……………………8分.
故原不等式化为: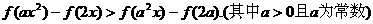 ,
,
即 … ………………………………………9分
… ………………………………………9分

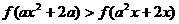 ,…………………………………………10分
,…………………………………………10分
又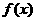 为
为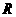 上的增函数;
上的增函数;

 ,即
,即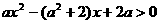
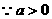 ,
,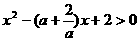

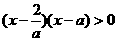 …………………11分
…………………11分
当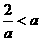 ,即
,即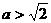 时,不等式的解集为
时,不等式的解集为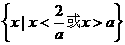 ;……12分
;……12分
当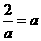 ,即
,即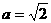 时,不等式的解集为
时,不等式的解集为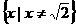 ;………………13分
;………………13分
当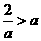 ,即
,即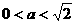 时,不等式的解集为
时,不等式的解集为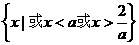 ………14分
………14分
8.(★★★★)已知函数f(x)=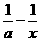 (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是增函数;
(2)若f(x)≤2x在(0,+∞)上恒成立,求a的取值范围;
(3)若f(x)在[m,n]上的值域是[m,n](m≠n),求a的取值范围.
7.(★★★★★)已知函数f(x)=6x–6x2,设函数g1(x)=f(x), g2(x)=f[g1(x)], g3(x)=f [g2(x)],
…gn(x)=f[gn–1(x)],…
(1)求证:如果存在一个实数x0,满足g1(x0)=x0,那么对一切n∈N,gn(x0)=x0都成立;
(2)若实数x0满足gn(x0)=x0,则称x0为稳定不动点,试求出所有这些稳定不动点;
(3)设区间A=(–∞,0),对于任意x∈A,有g1(x)=f(x)=a<0, g2(x)=f[g1(x)]=f(0)<0,
且n≥2时,gn(x)<0.试问是否存在区间B(A∩B≠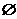 ),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
6.(★★★★)已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x–1)=f(3–x)且方程f(x)=2x有等根.
(1)求f(x)的解析式;
(2)是否存在实数m,n(m<n=,使f(x)定义域和值域分别为[m,n]和[4m,4n],如果存在,求出m、n的值;如果不存在,说明理由.
5.(★★★★)设集合A={x|4x–2x+2+a=0,x∈R}.
(1)若A中仅有一个元素,求实数a的取值集合B;
(2)若对于任意a∈B,不等式x2–6x<a(x–2)恒成立,求x的取值范围.
4.(★★★★★)如果y=1–sin2x–mcosx的最小值为–4,则m的值为 .
3.(★★★★)关于x的方程lg(ax–1)–lg(x–3)=1有解,则a的取值范围是 .
2.(★★★★★)函数f(x)的定义域为R,且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2–x+1,那么当x>1时,f(x)的递减区间是( )
A.[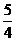 ,+∞
,+∞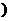 B.(1,
B.(1,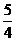
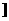 C.[
C.[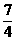 ,+∞
,+∞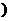 D.(1,
D.(1,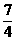 ]
]
1.(★★★★★)已知函数f(x)=loga[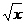 –(2a)2]对任意x∈[
–(2a)2]对任意x∈[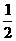 ,+∞]都有意义,则实数a的取值范围是( )
,+∞]都有意义,则实数a的取值范围是( )
A.(0,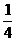
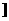 B.(0,
B.(0,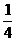 )
C.[
)
C.[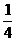 ,1
,1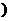 D.(
D.(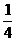 ,
,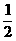 )
)
8.(★★★★)求函数f(x)=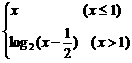 的不连续点和连续区间.
的不连续点和连续区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com