
题目列表(包括答案和解析)
3.设函数f(x)= ,则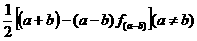 的值为
的值为
A、a B、b C、min{a,b}.D、max{a,b}
1.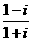 的虚部是( )
的虚部是( )
A、-i B、i C、-1 D、1
2已知全集U=Z,A={-2,-1,0,1},B={x |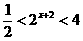 ,x∈Z},则
,x∈Z},则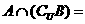 ( )
( )
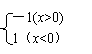 A、{0,1} B、{1} C、{-2,-1} D、{-1,0,1}
A、{0,1} B、{1} C、{-2,-1} D、{-1,0,1}
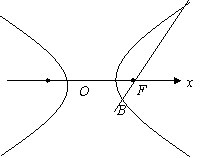
22.(本小题满分14分)
已知双曲线C的中心为坐标原点O,焦点在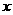 轴上,斜率为
轴上,斜率为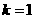 且经过双曲线的右焦点F的直线交双曲线于A、B两点,
且经过双曲线的右焦点F的直线交双曲线于A、B两点,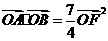 .
.
(1)求双曲线的离心率;
|
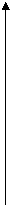 (2)设
(2)设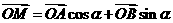 ,当
,当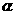 角在
角在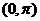 内变化时,试问:点M是否在双曲线C上?证明你的结论.
内变化时,试问:点M是否在双曲线C上?证明你的结论.
|
21.(本小题满分12分)
已知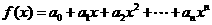
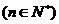 ,设
,设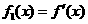 ,
,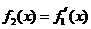 ,
,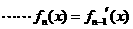 ,且
,且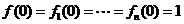 .
.
(1)求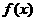 的解析式;
的解析式;
(2)求证: .
.
20.(本小题满分12分)
在等边三角形ABC中,O为中心,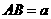 ,过O的直线交AB于M,交AC于N,若
,过O的直线交AB于M,交AC于N,若
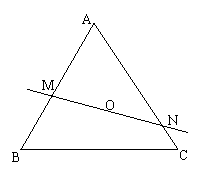
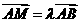 ,
,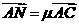 .
.
(1)证明: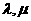 满足等式
满足等式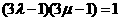 ;
;
(2)求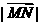 的最小值.
的最小值.
19.(本小题满分12分)
正四棱锥P-ABCD中,侧棱PA与底面所成的角的正切值为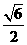 ,O为AC与BD的交点.
,O为AC与BD的交点.
(1)求侧面PAD与底面ABCD所成的角大小;
(2)若E为PB的中点,求PD、AE所成角的正切值;
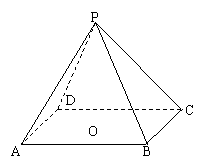 (3)在侧面PAD上找一点F,使EF
(3)在侧面PAD上找一点F,使EF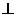 侧面PBC,确定F的位置并证明.
侧面PBC,确定F的位置并证明.
18.(本小题满分12分)
学校要从高二年级14个班中选出5名同学参加交流活动,若(1)、(13)、(14)班必须派一名同学参加,剩下2名在其余班级挑选(每班至多一名)。若用一次掷两枚骰子的方法,点数之和等于几则从这个班挑选,第二次掷若与第一次点数之和相等则再掷,直到确定了2个班级为止。
(1)问此种方法是否合理,说明理由;
(2)记随机变量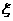 为掷一次骰子中点数之和,列出
为掷一次骰子中点数之和,列出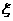 的概率分布列;
的概率分布列;
(3)求:若用以上方法一共掷了3次就确定了两个班级且(9)班和(3)班被选中的概率.(用分式表示)
17.(本小题满分12分)
函数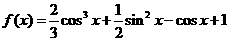 ,
,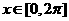 .
.
(1)求函数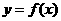 的最大值;
的最大值;
(2)写出函数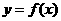 的单调区间.
的单调区间.
16.函数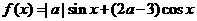 在
在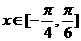 上恒为增函数,则实数
上恒为增函数,则实数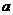 的取值范围为 .
的取值范围为 .
15.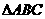 中,
中,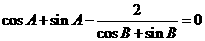 ,则边
,则边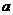 、
、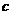 之比为 .
之比为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com