
题目列表(包括答案和解析)
7.某工程的工序流程如下表所示(工时数单位:天),则工程总时数为 天.
|
工序 |
a |
b |
c |
d |
e |
f |
|
紧前工序 |
-- |
a |
a,b |
c |
c |
d,e |
|
工时数(天) |
2 |
3 |
2 |
5 |
4 |
1 |
6.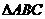 中,
中,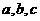 分别为角A,B,C的对边,若
分别为角A,B,C的对边,若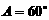 ,
,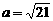 ,
,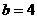 ,则边
,则边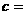 .
.
5.若圆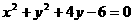 关于直线
关于直线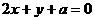 对称,则实数
对称,则实数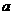 的值为_______.
的值为_______.
4.向量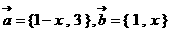 ,若
,若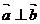 ,则实数
,则实数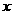 =_______.
=_______.
3.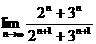 =___________.
=___________.
2.等差数列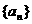 中,
中,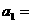 4,
4,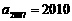 ,则公差
,则公差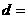 .
.
1.设集合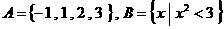 ,则A∩B =___________________.
,则A∩B =___________________.
22.(本小题满分16分)
(1) 当n >1时, bn = Bn –Bn – 1 = 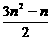 –
–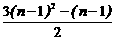 = 3n-2
= 3n-2
令n = 1得b1=1,
∴bn=3n-2. 5分
(2)由an= (1+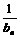 ) a
n – 1 ,得
) a
n – 1 ,得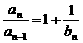 ∴an=
∴an=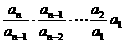
由a1 = 2 ,bn=3n-2知,
an=(1+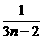 )(1 +
)(1 +
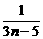 )…(1+
)…(1+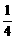 )2
)2
=(1+1)(1+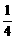 )…(1+
)…(1+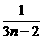 )
)
又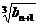 =
= 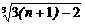 =
= 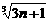 ,
5分
,
5分
设cn=
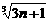 ,
,
当n=1时,有(1+1) = 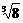 >
>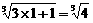
当n=2时,有an=(1+1)(1+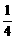 ) =
) = 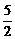 =
= 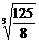 >
> 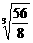 =
=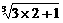 = cn
= cn
假设n=k(k≥1)时an>cn成立,即(1+1)(1+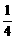 )…(1+
)…(1+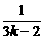 )>
)>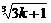 成立,
成立,
则n=k+1时,
左边== (1+1)(1+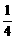 )…(1+
)…(1+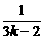 )(1+
)(1+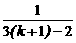 )
)
>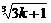 (1+
(1+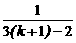 )=
)=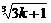
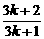 3分
3分
右边= c k +
1= 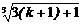 =
= 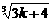
由(ak+1)3 – (c k + 1)3
=(3k + 1)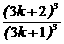 –(3k+4) =
–(3k+4) =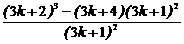
=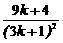 >0,
得ak+1 > c k
+ 1成立.
>0,
得ak+1 > c k
+ 1成立.
综合上述, an>cn对任何正整数n都成立. 3分
21. (本小题满分14分)
(1) 当| t | £ 2时,由x⊥y得:x·y = – k + (t2 – 3 ) t = 0,
得k = f (t ) = t3 – 3t ( | t | £ 2 )
当| t | >
2时, 由x∥y得: k = 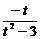
所以k = f (t ) =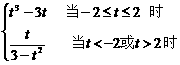 5分
5分
(2) 当| t | £ 2时, f `(t ) =3 t2 – 3 , 由f `(t ) < 0 , 得3 t2 – 3 < 0
解得 –1 < t < 1 ,
当| t | >
2时, f `(t ) = 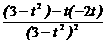 =
= 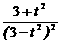 > 0
> 0
∴函数f (t )的单调递减区间是(–1, 1). 4分
(3) 当| t | £ 2时, 由f `(t ) =3 t2 – 3 =0得 t = 1或t = – 1
∵ 1 <| t | £ 2时, f `(t ) > 0
∴ f (t)极大值= f (–1) = 2, f (t)极小值= f (1) = –2
又 f ( 2 ) = 8 – 6 = 2, f (–2) = –8 + 6 = –2
当 t > 2 时, f (t ) =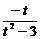 < 0 ,
< 0 ,
又由f `(t ) > 0知f (t )单调递增, ∴ f (t ) > f (2) = –2,
即当 t > 2 时, –2 < f (t ) < 0,
同理可求, 当t < –2时, 有0 < f (t ) < 2,
综合上述得, 当t = –1或t = 2时, f ( t )取最大值2
当t = 1或t = –2时, f ( t )取最小值–2 5分
20.(本小题满分14分)
设第n次取出白球的概率为Pn, 第n次取出红球的概率为Qn,
(1) 第二次取出红球的概率Q2 = 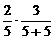 +
+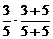 =
=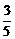 5分(每项2分)
5分(每项2分)
(2) 三次取的过程共有下列情况:
白白白,白红白,红白白,红红白,
第三次取出白球的概率
P3 = 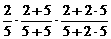 +
+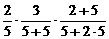 +
+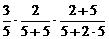 +
+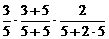
=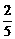 5分(每项1分)
5分(每项1分)
(3) 连续取球3次,得分的情况共有
5+5+5 , 5+8+5, 8+5+5, 8+8+5, 5+5+8 , 5+8+8, 8+5+8,8+8+8
列表如下:
|
x |
15 |
18 |
21 |
24 |
|
P |
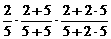 = 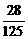 |
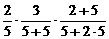 + +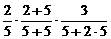 + +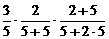 = 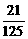 |
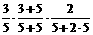 + +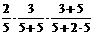 + +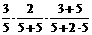 = 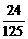 |
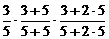 = =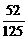 |
得分期望x = 15´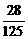 + 18´
+ 18´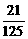 +21´
+21´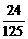 + 24´
+ 24´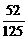 =
= 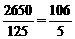 4分
4分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com