
题目列表(包括答案和解析)
8. 已知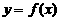 是周期为
是周期为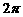 的函数, 当
的函数, 当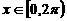 时,
时, 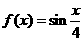 , 则方程
, 则方程
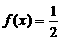 的解集为
的解集为
(A) 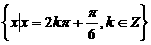 (B)
(B) 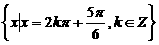
(C) 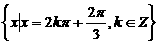 (D)
(D) 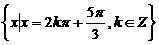
7. 若一系列函数的解析式相同,值域相同但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为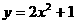 ,值域为
,值域为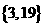 的“孪生函数”共有
的“孪生函数”共有
(A) 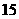 个 (B)
个 (B) 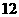 个 (C)
个 (C) 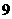 个 (D)
个 (D) 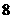 个
个
6. 已知过抛物线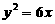 焦点的弦长为
焦点的弦长为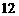 ,则此弦所在直线的倾斜角是
,则此弦所在直线的倾斜角是
(A) 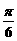 或
或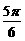 (B)
(B) 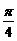 或
或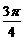 (C)
(C) 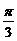 或
或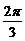 (D)
(D) 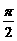
5. 函数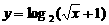 的反函数是
的反函数是
(A) 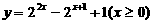 (B)
(B) 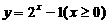
(C) 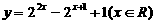 (D)
(D) 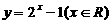
4. 已知直线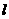 与平面
与平面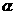 成
成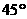 角,直线
角,直线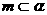 ,若直线
,若直线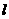 在
在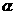 内的射影与直线
内的射影与直线 也成
也成
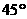 角,则
角,则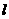 与
与 所成的角是
所成的角是
(A) 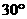 (B)
(B) 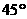 (C)
(C)  (D)
(D) 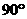
3.  是
是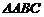 内一点,
内一点, 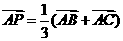 , 则
, 则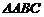 的面积与
的面积与 的面积之比为
的面积之比为
(A) 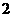 (B)
(B)
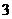 (C)
(C) 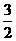 (D)
(D) 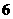
2. “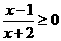 ”是“
”是“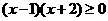 ”的
”的
(A) 充要条件 (B) 充分不必要条件
(C) 必要不充分条件 (D) 既不充分也不必要条件
1. 已知复数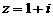 , 则
, 则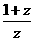 等于
等于
(A) 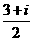 (B)
(B) 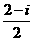 (C)
(C) 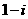 (D)
(D) 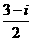
22.(本题满分18分.第(1)题4分,第(2)题14分,分别为4、4、6分)
已知抛物线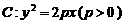 上横坐标为
上横坐标为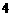 的点到焦点的距离为
的点到焦点的距离为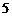 .
.
(1)求抛物线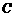 的方程.
的方程.
(2)设直线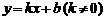 与抛物线
与抛物线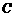 交于两点
交于两点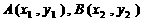 ,且
,且
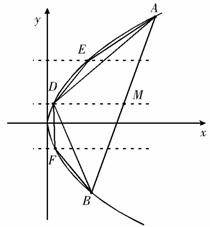
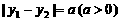 ,
,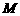 是弦
是弦 的中点,过
的中点,过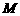 作平行于
作平行于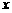 轴的直线交抛物线
轴的直线交抛物线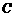 于点
于点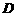 ,得到
,得到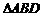 ;再分别过弦
;再分别过弦 、
、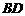 的中点作平行于
的中点作平行于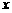 轴的直线依次交抛物线
轴的直线依次交抛物线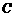 于点
于点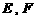 ,得到
,得到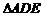 和
和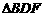 ;按此方法继续下去.
;按此方法继续下去.
解决下列问题:
1 求证: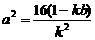 ;
;
2 计算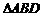 的面积
的面积 ;
;
3 根据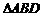 的面积
的面积 的计算结果,写出
的计算结果,写出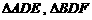
的面积;请设计一种求抛物线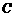 与线段
与线段 所围成封闭图
所围成封闭图
形面积的方法,并求出此封闭图形的面积.
21.(本题满分16分,第(1)题4分,第(2)题7分,第(3)题5分)
记函数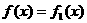 ,
,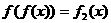 ,它们定义域的交集为
,它们定义域的交集为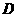 ,若对任意的
,若对任意的
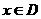 ,
,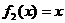 ,则称
,则称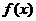 是集合
是集合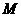 的元素.
的元素.
(1)判断函数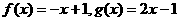 是否是
是否是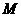 的元素;
的元素;
(2)设函数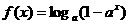 ,求
,求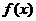 的反函数
的反函数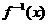 ,并判断
,并判断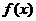 是否是
是否是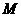 的元素;
的元素;
(3)若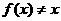 ,写出
,写出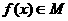 的条件,并写出两个不同于(1)、(2)中的函数.(将根据写出的函数类型酌情给分)
的条件,并写出两个不同于(1)、(2)中的函数.(将根据写出的函数类型酌情给分)
[解]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com