4.(★★★★)命题A：两曲线F(x,y)=0和G(x,y)=0相交于点P(x₀,y₀),命题B：曲线F(x,y)+λG(x,y)=0(λ为常数)过点P(x₀,y₀),则A是B的__________条件.

3.(★★★★)a=3是直线ax+2y+3a=0和直线3x+(a－1)y=a－7平行且不重合的_________.

2.(★★★★)“a=1”是函数y=cos²ax－sin²ax的最小正周期为“π”的(　　 )

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既非充分条件也不是必要条件

1.(★★★★)函数f(x)=x|x+a|+b是奇函数的充要条件是(　　 )

A.ab=0　　　　　　　　　　　　 B.a+b=0　　　　　　　　　　　 C.a=b　　　　　　　　　 D.a²+b²=0

3. (安徽卷)已知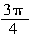＜α＜π，tanα+cotα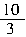＝－. 　(1)求tanα的值； 　(2)求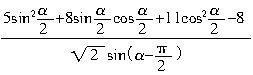的值.

解析：(1)由tanα+cotα＝－得3tan2α+10tanα+3＝0，即tanα＝－3或tanα＝－， 　又＜α＜π，所以tanα＝－=为所求. 　

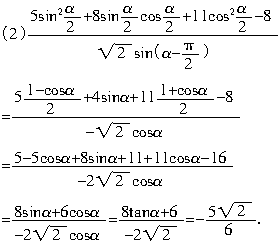
2. (广东卷)已知等差数列共有10项，其中奇数项之和为15，偶数项之和为30，则其公差是( ). 　A. 5　　B. 4　　C. 3　　D. 2

　解析：设等差数列的首项为a₁，公差为d据题意得：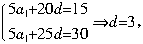

　答案：C

　 点评：运用等差、等比数列的基本量(a₁，d，q)列方程，方程组是求解数列基本问题的通法.

3. 设t＝|x²－1|(t≥0)，t²－t+k＝0，方程的判别式为Δ＝1－4k，由k的取值依据Δ＞0、△＝0、△＜0从而得出解的个数. 　4. 设函数f(x)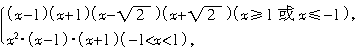＝，利用数轴标根法得出函数与x轴的交点个数为5个，以及函数的单调性大体上画出函数的图象，从而得出答案A.

　答案：A

　 点评：思路1、思路2、思路4都是利用函数图象求解，但研究的目标函数有别，思路2利用函数的奇偶性以及交轨法直观求解，很好地体现了数形结合的数学思想，是数形结合法中值得肯定的一种方法；思路3利用方程的根的个数问题去求解，但讨论较为复杂，又是我们的弱点，有利于培养我们思维的科学性、严谨性、抽象性、逻辑推理能力等基本素质.

1. (湖北卷)关于x的方程(x²－1)²－|x²－1|+k＝0，给出下列四个命题： 　①存在实数k，使得方程恰有2个不同的实根； 　②存在实数k，使得方程恰有4个不同的实根； 　③存在实数k，使得方程恰有5个不同的实根； 　④存在实数k，使得方程恰有8个不同的实根. 　其中假命题的个数是(　　 ). 　A. 0　　B. 1　　C. 2　　D. 4

　解析：本题是关于函数、方程解的选择题，考查换元法及方程根的讨论，属一题多选型试题，要求考生具有较强的分析问题和解决问题的能力. 　思路分析： 　1. 根据题意可令｜x²－1｜＝t(t≥0)，则方程化为t²－t+k＝0，(*) 作出函数t＝｜x²－1｜的图象，结合函数的图象可知①当t＝0或t＞1时，原方程有两上不等的根，②当0＜t＜1时，原方程有4个根，③当t＝1时，原方程有3个根. 　(1)当k＝－2时，方程(*)有一个正根t＝2，相应的原方程的解有2个； 　(2)当k＝时，方程(*)有两个相等正根t＝，相应的原方程的解有4个； 　(3)当k＝0时，此时方程(*)有两个不等根t＝0或t＝1，故此时原方程有5个根； 　(4)当0＜k＜时，方程(*)有两个不等正根，且此时方程(*)有两正根且均小于1，故相应的满足方程|x²－1|＝t的解有8个，故选A. 　2. 由函数f(x)＝(x²－1)²－|x²－1|的图象(如下图)及动直线g(x)＝k可得出答案为A.

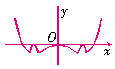
3．函数方程思想的几种重要形式

(1)函数和方程是密切相关的，对于函数y＝f(x)，当y＝0时，就转化为方程f(x)＝0，也可以把函数式y＝f(x)看做二元方程y－f(x)＝0。

(2)函数与不等式也可以相互转化，对于函数y＝f(x)，当y＞0时，就转化为不等式f(x)＞0，借助于函数图像与性质解决有关问题，而研究函数的性质，也离不开解不等式；

(3)数列的通项或前n项和是自变量为正整数的函数，用函数的观点处理数列问题十分重要；

(4)函数f(x)＝(1+x)^n (n∈N^*)与二项式定理是密切相关的，利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题；

(5)解析几何中的许多问题，例如直线和二次曲线的位置关系问题，需要通过解二元方程组才能解决，涉及到二次方程与二次函数的有关理论；

(6)立体几何中有关线段、角、面积、体积的计算，经常需要运用布列方程或建立函数表达式的方法加以解决。

2　　　　　 经典例题剖析

(根据近几年高考命题知识点及热点做相应的试题剖析，要求例题不得少于8个)

2．方程的思想，就是分析数学问题中变量间的等量关系，建立方程或方程组，或者构造方程，通过解方程或方程组，或者运用方程的性质去分析、转化问题，使问题获得解决。方程思想是动中求静，研究运动中的等量关系；