
题目列表(包括答案和解析)
1. 已知集合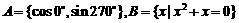 则
则 为
为
A. 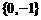 B.
B.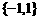 C.
C.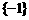 D.
D.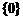
(16).(本小题满分12分)
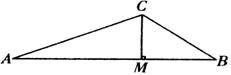 如图,在△ABC中,角A、B、C的对边分别为
如图,在△ABC中,角A、B、C的对边分别为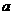 、
、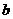 、c,
、c,
且8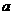 =7
=7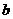 ,
,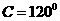 ,AB边上的高CM长为
,AB边上的高CM长为 .
.
(Ⅰ)求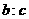 的值;
(Ⅱ)求△ABC的面积
的值;
(Ⅱ)求△ABC的面积
(17).(本小题满分12分)
设数列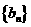 的前
的前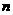 项和为
项和为 ,且
,且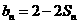 ;数列
;数列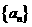 为等差数列,且
为等差数列,且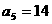 ,
,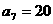 .
.
(Ⅰ)求数列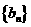 的通项公式;
的通项公式;
(Ⅱ)若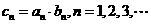 ,
, 为数列
为数列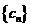 的前
的前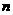 项和. 求证:
项和. 求证: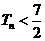 .
.
(18).(本小题满分14分)
有10张形状、大小相同的卡片,其中2张上写着数字 ,另外5张上写着数字1,余下3张上写着数字2。从中随机地取出1张,记下它的数字后放回原处。当这种手续重复进行2次时,
,另外5张上写着数字1,余下3张上写着数字2。从中随机地取出1张,记下它的数字后放回原处。当这种手续重复进行2次时,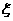 为所记下的两个数之和。
为所记下的两个数之和。
(Ⅰ)求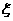 =2时的概率;
(Ⅱ)求
=2时的概率;
(Ⅱ)求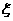 的数学期望;
的数学期望;
(19).(本小题满分14分)
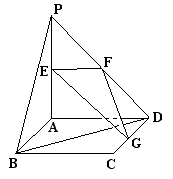 如图,平面
如图,平面 ⊥平面
⊥平面 ,
, 为正方形,
为正方形,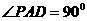 ,
,
且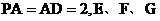 分别是线段
分别是线段 的中点。
的中点。
(Ⅰ)求证: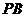 //平面
//平面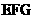 ;
;
(Ⅱ)求异面直线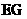 与
与 所成的角;
所成的角;
(Ⅲ)在线段 上是否存在一点
上是否存在一点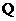 ,使得点
,使得点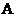 到平面
到平面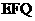 的距离为
的距离为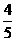 ;
;
若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(20).(本小题满分14分)
已知椭圆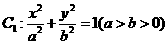 的离心率为
的离心率为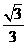 ,直线
,直线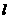 :
: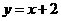 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左焦点为
的左焦点为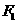 ,右焦点
,右焦点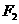 ,直线
,直线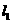 过点
过点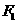 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直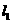 于点
于点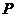 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹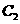 的方程;
的方程;
(Ⅲ)设 (Ⅱ) 中的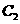 与
与 轴交于点
轴交于点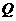 ,不同的两点
,不同的两点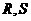 在
在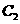 上,且满足
上,且满足 求
求 的取值范围.
的取值范围.
(21).(本小题满分14分)
已知 、b为函数
、b为函数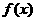 的极值点
的极值点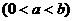
(Ⅰ)求证: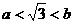 ;
;
(Ⅱ)判断函数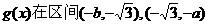 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅲ)若曲线 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程 有两个不等的实根,求实数
有两个不等的实根,求实数 的取值范围.
的取值范围.
(9).若 为等差数列
为等差数列 中的第8项,则二项式
中的第8项,则二项式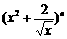 展开式中常数项是第 项.
展开式中常数项是第 项.
(10).定义在R上的奇函数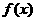 满足:对于任意
满足:对于任意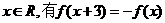 ,若
,若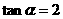 ,
,
 __________.
__________.
(11).定义 是向量a和b的“向量积”,它的长度
是向量a和b的“向量积”,它的长度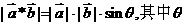 为向量a和b的夹角,若
为向量a和b的夹角,若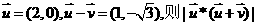 =
.
=
.
(12).有以下四个命题:
①两直线m,n与平面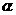 所成的角相等的充要条件是m//n;
所成的角相等的充要条件是m//n;
②若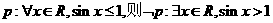 ;
;
③不等式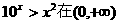 上恒成立;
上恒成立;
④设有四个函数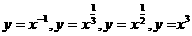 ,其中在R上是增函数的函数有3个.
,其中在R上是增函数的函数有3个.
其中真命题的序号是 .(漏填、多填或错填均不得分)
(13).(坐标系与参数方程选做题)已知极坐标系的极点 与直角坐标系的原点重合,极轴与
与直角坐标系的原点重合,极轴与 轴的正半轴重合,线
轴的正半轴重合,线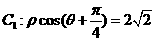 与线
与线 (参数
(参数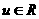 )交于
)交于 、
、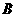 两点.
两点.
写出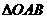 的外接圆的标准方程
.
的外接圆的标准方程
.
(14).(不等式选讲选做题)
已知方程 的两根分别为1和2,则不等式
的两根分别为1和2,则不等式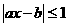 的解集为 (用区间表示).
的解集为 (用区间表示).
 (15).(几何证明选讲选做题)从⊙
(15).(几何证明选讲选做题)从⊙ 外一点
外一点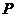 向圆引两条切线
向圆引两条切线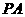 、
、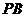 (
( 、
、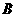 为切点)和割线
为切点)和割线
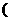 与⊙
与⊙ 交于
交于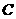 、
、 两点
两点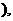 从
从 点作弦
点作弦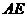 平行于
平行于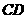 ,连结
,连结 交
交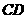 于
于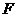 ,连结
,连结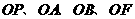 ,若
,若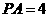 ,
, ,则
,则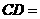 .
.
(1).复数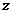 满足方程:
满足方程: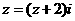 ,则
,则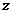 =
=
(A).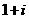 (B).
(B).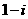 (C).
(C).
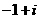 (D).
(D).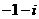
(2).已知集合 ,R是实数集,则
,R是实数集,则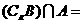 ( )
( )
(A).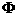 (B).R
(C).
(B).R
(C).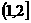 (D).
(D).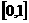
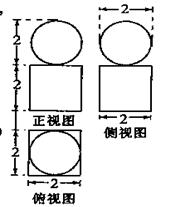
(3).右图表示一个几何体的三视图及相应数据,则该几何体的体积是 ( )
(A). (B).
(B).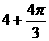 (C).
(C).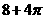 (D).
(D). 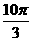
(4).偶函数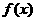 在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,
在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,
则方程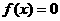 在区间[-a,a]内根的个数是
( )
在区间[-a,a]内根的个数是
( )
(A). 3 (B). 2 (C). 1 (D). 0
(5).给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b ”类比推出“若a,b
”类比推出“若a,b ”;
”;
②“若a,b,c,d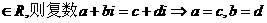 ”类比推出“若a,b,c,d
”类比推出“若a,b,c,d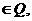
则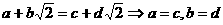 ”;
”;
③“若a,b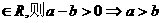 ” 类比推出“若a,b
” 类比推出“若a,b ”;
”;
其中类比结论正确的个数是 ( )
(A).0 (B).1 (C).2 (D).3
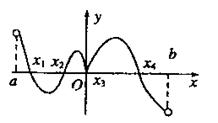 (6).函数
(6).函数 的定义域为(a,b),其导函数
的定义域为(a,b),其导函数 内的图象如图所示,
内的图象如图所示,
则函数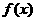 在区间(a,b)内极小值点的个数是( )
在区间(a,b)内极小值点的个数是( )
(A).1 (B).2 (C).3 (D).4
(7).已知F1,F2分别是双曲线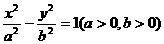 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐用三角形,则该双曲线离心率的取值范围是( )
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐用三角形,则该双曲线离心率的取值范围是( )
(A).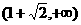 (B).
(B).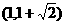 (C).
(C). (D).
(D).
(8).2006年1月开始实施的《个人所得税法》规定:全月总收入不超过1600元的免征个人工资、薪金所得税,超过1600元的部分需征税,设全月总收入金额为x元,前三级税率如下表:
|
级数 |
全月应纳税金额 x-1600元 |
|
||
|
1 |
不超过500元部分 |
5% |
||
|
2 |
超过500元至2000元部分 |
10% |
||
|
3 |
超过2000元至5000元部分 |
15% |
||
|
…… |
…… |
…… |
当全月总收入不超过3600元时,计算个人所得税的一个
算法框图如上所示,则输出①,输出②分别为 ( )
(A).0.05x,0.1x (B).0.05x, 0.1x-185
(C).0.05x-80, 0.1x (D).0.05x-80, 0.1x-185
22.(本小题满分16分)
(1) 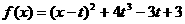 , 当
, 当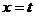 时,
时, 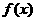 达到其最小值
达到其最小值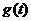 ,即
,即
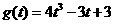 ;
--- 4分
;
--- 4分
(2)因为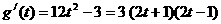 ,
,
列表如下:
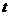 |
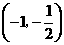 |
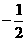 |
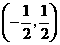 |
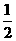 |
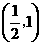 |
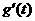 |
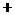 |
 |
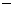 |
 |
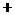 |
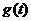 |
|
极大值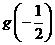 |
|
极小值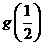 |
|
由此可见,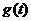 在区间
在区间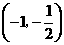 和
和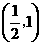 单调递增,在区间
单调递增,在区间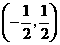 单调递减; --- 6分
单调递减; --- 6分
(3) 
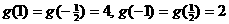 ,所以
,所以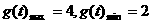 ;
;
又
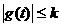 既
既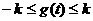 恒成立,所以
恒成立,所以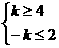 ,综合可得k的范围为:
,综合可得k的范围为: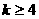 .
.
--- 6分
21.(本小题满分14分)
(1) 当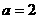 时, 不等式化为
时, 不等式化为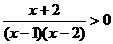 , ---
2分
, ---
2分
所以不等式的解集为
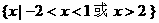 ;
--- 3分
;
--- 3分
(2) 当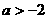 时, 不等式可化为
时, 不等式可化为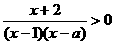 , ---
3分
, ---
3分
当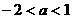 时, 解集为
时, 解集为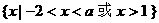 ;
--- 2分
;
--- 2分
当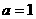 时, 解集为
时, 解集为 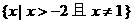 ;
--- 2分
;
--- 2分
当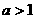 时, 解集为
时, 解集为 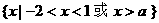 .
--- 2分
.
--- 2分
20. (本小题满分14分)
(1)
由题意知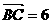 a0,
a0, 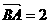 b0, ∴
b0, ∴ 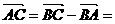 6 a0 - 2 b0;
6 a0 - 2 b0;
∵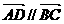 , ∴
, ∴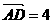 a0, 则
a0, 则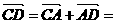 2
b0 - 6 a0 + 4 a0 = 2 b0 - 2 a0 ;
2
b0 - 6 a0 + 4 a0 = 2 b0 - 2 a0 ;
--- 4分
∵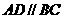 , ∴
, ∴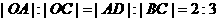 ,
,
则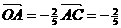 (6 a0 - 2 b0) =
(6 a0 - 2 b0) = 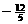 a0
a0 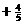 b0 .
--- 4分
b0 .
--- 4分
(2) 由题意知点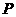 是在以点
是在以点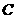 为圆心, 3为半径的圆周上运动, 所以由几何意义即得
为圆心, 3为半径的圆周上运动, 所以由几何意义即得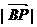 的最大值和最小值分别应该为8和4.
--- 6分
的最大值和最小值分别应该为8和4.
--- 6分
19. (本小题满分14分)
(1)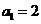 ,
,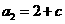 ,
,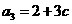 ,
--- 2分
,
--- 2分
∵ ,
,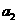 ,
,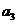 成等比数列,∴
成等比数列,∴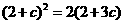 ,
--- 2分
,
--- 2分
解得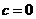 或
或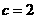 , 当
, 当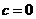 时,
时,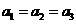 ,不符合题意舍去,故
,不符合题意舍去,故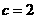 . --- 3分
. --- 3分
(2)当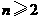 时,∵
时,∵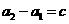 ,
,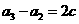 ,
,
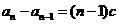 ,
,
∴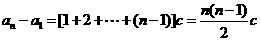 .
--- 3分
.
--- 3分
又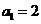 ,
,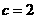 ,故
,故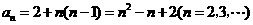 .
--- 3分
.
--- 3分
当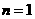 时,上式也成立,所以
时,上式也成立,所以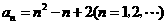 . ---
1分
. ---
1分
18. (本小题满分14分)
(1) ∵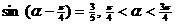 , ∴
, ∴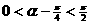 , 有
, 有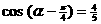 ; --- 4分
; --- 4分
(2) 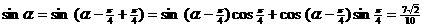 ;
--- 5分
;
--- 5分
(3) 函数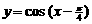 的图象可以通过函数
的图象可以通过函数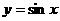 的图象向左平移
的图象向左平移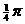 个单位得到.
个单位得到.
. --- 5分
15.  ,
,  16.
45
17. ① ② ④
16.
45
17. ① ② ④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com