
题目列表(包括答案和解析)
7.(2005年高考·福建卷·理12)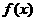 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且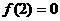 则方程
则方程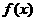 =0在区间(0,6)内解的个数的最小值是 ( D )
=0在区间(0,6)内解的个数的最小值是 ( D )
A.2 B.3 C.4 D.5
6.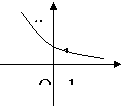 (2005年高考·福建卷·理5文6)函数
(2005年高考·福建卷·理5文6)函数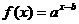 的图象如图,其中a、b为常数,则下列结论正确的是 ( D )
的图象如图,其中a、b为常数,则下列结论正确的是 ( D )
A.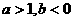 B.
B.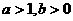
C.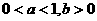 D.
D.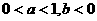
5.(2005年高考·上海卷·理16)设定义域为R的函数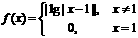 ,则关于
,则关于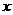 的方程
的方程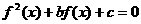 有7个不同实数解的充要条件是 ( C )
有7个不同实数解的充要条件是 ( C )
A.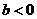 且
且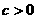 B.
B.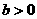 且
且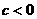 C.
C.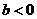 且
且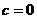 D.
D.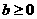 且
且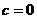
4.(2005年高考·上海卷·理13文13)若函数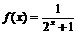 ,则该函数在
,则该函数在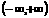 上是 ( A )
上是 ( A )
A.单调递减无最小值 B.单调递减有最小值
C.单调递增无最大值 D.单调递增有最大值
3. (2005年春考·上海卷16)设函数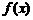 的定义域为
的定义域为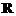 ,有下列三个命题:
,有下列三个命题:
(1)若存在常数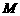 ,使得对任意
,使得对任意 ,有
,有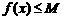 ,则
,则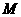 是函数
是函数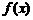 的最大值;
的最大值;
(2)若存在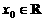 ,使得对任意
,使得对任意 ,且
,且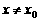 ,有
,有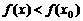 ,则
,则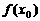 是函数
是函数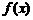
的最大值;
(3)若存在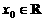 ,使得对任意
,使得对任意 ,有
,有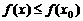 ,则
,则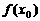 是函数
是函数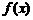 的最大值.
的最大值.
这些命题中,真命题的个数是 ( C )
A.0个 B.1个 C.2个 D.3个
2.
 (2005年春考·北京卷·文2)函数
(2005年春考·北京卷·文2)函数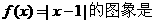 ( B )
( B )
1.(2005年春考·北京卷·理2)函数y=|log2x|的图象是 ( A )
[例1] 关于x的不等式2·32x–3x+a2–a–3>0,当0≤x≤1时恒成立,则实数a的取值范围为 .
解:设t=3x,则t∈[1,3],原不等式可化为a2–a–3>–2t2+t,t∈[1,3].
等价于a2–a–3大于f(t)=–2t2+t在[1,3]上的最大值.
答案:(–∞,–1)∪(2,+∞)
[例2]
设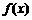 是定义在
是定义在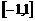 上的奇函数,
上的奇函数,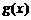 的图象与
的图象与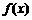 的图象关于直线
的图象关于直线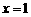 对称,而当
对称,而当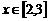 时,
时,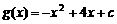 (c为常数)。
(c为常数)。
(1)求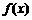 的表达式;
的表达式;
(2)对于任意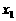 ,
,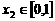 且
且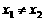 ,求证:
,求证: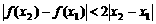 ;
;
(3)对于任意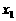 ,
,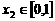 且
且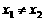 ,求证:
,求证: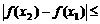 1.
1.
解:(1)设g(x)上点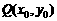 与f(x)上点P(x,y)对应,
与f(x)上点P(x,y)对应,
∴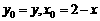 ;∵
;∵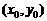 在g(x)图象上
在g(x)图象上
∴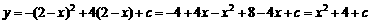
∵g(x)定义域为x∈[2,3],而f(x)的图象与g(x)的图象关于直线x=1对称,
所以,上述解析式是f(x)在[–1,0]上的解析式
∵f(x)是定义在[–1,1]上的奇函数,∴f(0)=0,∴c=–4
所以,当x∈[0,1]时,–x∈[–1,0],f(x)=–f(–x)=–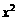
所以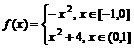
(2)当x∈[0,1]时,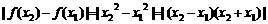
∵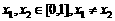 ,∴
,∴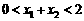 ,所以
,所以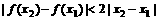
(3)∵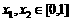 ,∴
,∴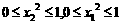
∴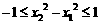 ,∴
,∴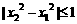
即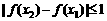
[例3]
已知函数f(x)=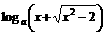 (a>0, a≠1)
(a>0, a≠1)
(1) 求反函数f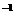 (x),并求出其定义域。
(x),并求出其定义域。
(2) 设P(n)=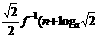 ),如果P(n)<
),如果P(n)<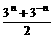 (n∈N),求a的取值范围。
(n∈N),求a的取值范围。
解:(1) 设y= f(x)=log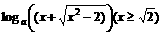
∴ay=x+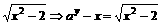
两端平方整理得:a2y-2xay+2=0Þx=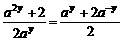
∴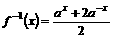 ∵a>1时,f(x)=
∵a>1时,f(x)=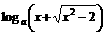 值域为
值域为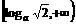
0<a<1时,f(x)的值域为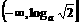
∴ f-1 (x)的定义域为:a>1时,x∈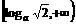 0<a<1时,x∈
0<a<1时,x∈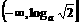
(2) P(n)=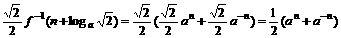
由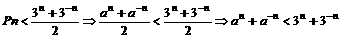
即an+a-n-(3n-3-n)=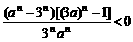
∵(3a)n>0 ∴(an-3n)[(3a)n-1]<0Þ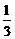 <a<3;
<a<3;
又∵n∈N,∴n+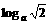 >
>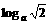 Þa>1
Þa>1
即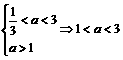
[例4]
设函数f(x)的定义域关于原点对称,且满足①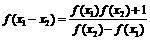 ②存在正常数a,使f(a) = 1,求证:(1)f(x)为奇函数;(2)f(x)为周期函数,且一个周期为4a。
②存在正常数a,使f(a) = 1,求证:(1)f(x)为奇函数;(2)f(x)为周期函数,且一个周期为4a。
证明:(1)令x =x1 - x2
则f( - x) = f ( x2
- x1)=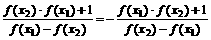
= -f (x1 -x2 )= -f (x),∴f (x)为奇函数。
(2)∵f( x+a ) = f[x - ( -a ) ]=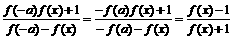
∴f (x+2a )=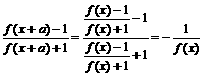
∴f ( x+4a)=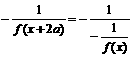 =f (x)
=f (x)
∴f (x)是以4a为周期的周期函数。
[例5]
已知函数f(x)=logm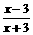
(1)若f(x)的定义域为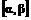 ,(β>α>0),判断f(x)在定义域上的增减性,并加以说明;
,(β>α>0),判断f(x)在定义域上的增减性,并加以说明;
(2)当0<m<1时,使f(x)的值域为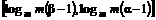 的定义域区间为
的定义域区间为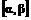
(β>α>0)是否存在?请说明理由.
解:(1)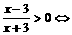 x<–3或x>3.
x<–3或x>3.
∵f(x)定义域为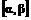 ,∴α>3
,∴α>3
设β≥x1>x2≥α,有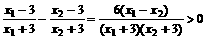
当0<m<1时,f(x)为减函数,当m>1时,f(x)为增函数.
(2)若f(x)在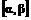 上的值域为
上的值域为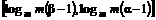
∵0<m<1, f(x)为减函数.
∴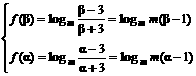
即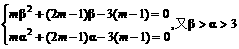
即α,β为方程mx2+(2m–1)x–3(m–1)=0的大于3的两个根
∴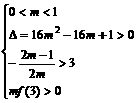 ∴0<m<
∴0<m<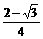
故当0<m<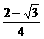 时,满足题意条件的m存在.
时,满足题意条件的m存在.
[例6] 已知函数f(x)=x2–(m+1)x+m(m∈R)
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角.求证:m≥5;
(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
解: (1)证明:f(x)+4=0即x2–(m+1)x+m+4=0.依题意:
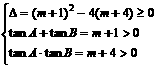 又A、B锐角为三角形内两内角
又A、B锐角为三角形内两内角
∴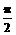 <A+B<π
<A+B<π
∴tan(A+B)<0,即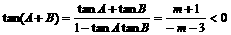
∴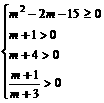 ∴m≥5
∴m≥5
(2)证明:∵f(x)=(x–1)(x–m)
又–1≤cosα≤1,∴1≤2+cosα≤3,恒有f(2+cosα)≤0
即1≤x≤3时,恒有f(x)≤0即(x–1)(x–m)≤0
∴m≥x但xmax=3,∴m≥xmax=3
(3)解:∵f(sinα)=sin2α–(m+1)sinα+m=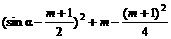
且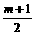 ≥2,∴当sinα=–1时,f(sinα)有最大值8.
≥2,∴当sinα=–1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3
[例7]
已知函数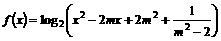 的定义域为实数集。(1)求实数m的所有允许值组成的集合M;(2)求证:对所有
的定义域为实数集。(1)求实数m的所有允许值组成的集合M;(2)求证:对所有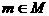 ,恒有
,恒有 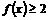 。
。
证明(1)∵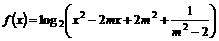 的定义域为实数集
的定义域为实数集
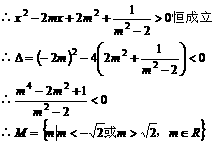
(2)令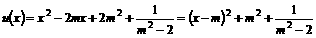
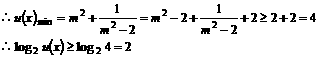
[例8]
设 =
=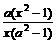 ,(a>0,a≠1),求证:(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;(2)f(3)>3。
,(a>0,a≠1),求证:(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;(2)f(3)>3。
解:(1)令t=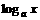 ,则x=
,则x=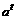 ,f(x)=
,f(x)= 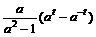 (t∈R)
(t∈R)
∴f(x)= 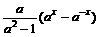 (x∈R)
(x∈R)
设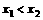 ,f(
,f(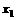 )-f(
)-f(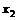 )=
)=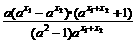
(1)a>1时,…,f(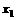 )<f(
)<f(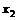 ),∴f(x)在(-∞,+∞)上单调递增
),∴f(x)在(-∞,+∞)上单调递增
(2)0<a<1时,…,f(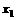 )<f(
)<f(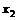 ),∴f(x)在(-∞,+∞)上单调递增
),∴f(x)在(-∞,+∞)上单调递增
∴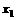 <
<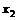 时,恒有f(
时,恒有f(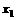 )<f(
)<f(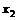 ),∴K=
),∴K=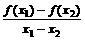 >0
>0
(2)f(3)=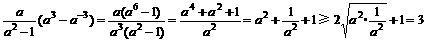
∵a>0,a≠1 ∴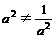 ∴上述不等式不能取等号,∴f(x)>3
∴上述不等式不能取等号,∴f(x)>3
[例9]
已知函数f(x)=lg(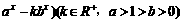 的定义域为(0,+∞),问是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(3)=lg4,若存在,求出a,b的值,若不存在,说明理由。
的定义域为(0,+∞),问是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(3)=lg4,若存在,求出a,b的值,若不存在,说明理由。
解:由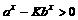 ,得
,得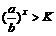 ,∵a>1>b>0,∴
,∵a>1>b>0,∴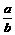 >1,∴x>log
>1,∴x>log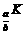
又f(x)定义域为(0,+∞),∴log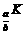 =0,K=1,∴f(x)=lg
=0,K=1,∴f(x)=lg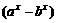
设0<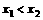 ,
,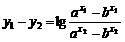 ,∵a>1>b>0,∴a
,∵a>1>b>0,∴a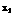 < a
< a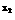 ,-b
,-b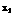 < b
< b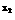
∴0< a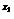 -b
-b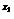 < a
< a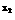 - b
- b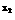 ,∴0<
,∴0<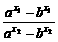 <1,∴lg
<1,∴lg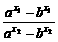 <0
<0
∴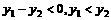 ,∴f(x)在(0,+∞)上是增函数
,∴f(x)在(0,+∞)上是增函数
∴x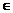 (1,+∞)时,必有f(x)>f(1)=lg(a-b)
(1,+∞)时,必有f(x)>f(1)=lg(a-b)
∵f(x)在(1,+∞)上取正值,∴lg(a-b)=0 a-b=1 (1)
又f(3)=lg4 ∴lg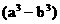 =lg4,
=lg4,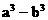 =4 (2)
=4 (2)
解(1)(2)得: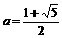 ,b=
,b=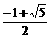 ,即有在
,即有在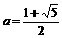 ,b=
,b=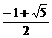 满足条件
满足条件
[例10] 设二次函数f(x)= ax2 +bx+c (a>0且b≠0)。
(1) 已知|f(0)|=|f(1)|=|f(-1)|=1,试求f(x)的解析式和f(x)的最小值;
(2) 已知f(x)的对称轴方程是x=1,当f(x)的图象在x轴上截得的弦长不小于2时,试求a, b, c满足的条件;
(3) 已知|b|<a, |f(0)| 1, |f(-1)|
1, |f(-1)| 1, |f(1)|
1, |f(1)| 1,当|x|
1,当|x| 1时,证明:|f(x)|
1时,证明:|f(x)|
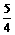
解:(1)由|f(0)|=|f(1)|=|f(-1)|知|c|=1,|a+b+c|=1,|a-b+c|=1
∴(a+b+c)2=(a-b+c)2即4(a+c)b=0
∵b≠0 ∴a+c=0,即:a=-c
又∵a>0 ∴a=1 c=-1 此时b=+1 ∴f(x)=x2 + x-1
于是 f(x)=(x + 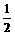 )2
)2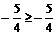 ∴[f(x)]
∴[f(x)]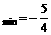
(2)依题意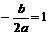 即b=-2a,∵a>0且b≠0 ∴b<0
即b=-2a,∵a>0且b≠0 ∴b<0
令f(x)=0的两根为x1,x2,则函数y=f(x)的图象与x轴的两个交点为(x1,0),(x2,0)
且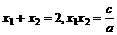 ,满足题设的充要条件是
,满足题设的充要条件是
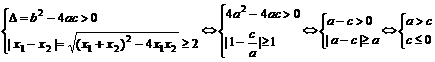
∴a>0 c 0 b<0且b=-2a为所求
0 b<0且b=-2a为所求
(3)方法1:
∵|2b|=|(a+b+c)-(a-b+c)|<|a+b+c|+|a-b+c|<2 ∴|b| 1 又|b|
1 又|b| |a| ∴
|a| ∴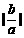
 1
1
又|c|=|f(0)| 1 又|f(
1 又|f(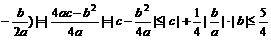
而f(x)所示开口向上的抛物线且|x|<1,则|f(x)|的最大值应在x=1或x=-1或x=-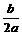 时取到,因|f(-1)|<1,
|f(1)|
时取到,因|f(-1)|<1,
|f(1)| 1, |f(-
1, |f(-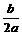 )|
)|
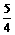 故|f(x)|
故|f(x)|
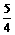 得证。
得证。
方法2:
令f(x)=uf(1)+vf(-1)+(1-u-v)f(0) 则f(x)=(a+b+c)u+(a-b+c)v+(1-u-v)c
ax2 +bx+c=a(u+v)+b(u-v)+c
∴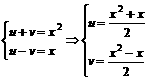
∴f(x)=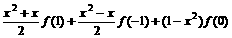
而|f(1)|
 1, |f(-1)|
1, |f(-1)| 1, |f(0)|
1, |f(0)| 1
1
∴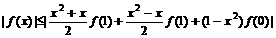 <
<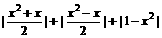 x∈[-1, 1]
x∈[-1, 1]
=|x|·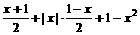 =
=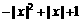 =
=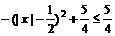
综上,当|f(0)| 1, |f (-1)|
1, |f (-1)| 1, |f(-1)|
1, |f(-1)| 1, |x|
1, |x| 1时,|f(x)|
1时,|f(x)|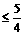
解法3:我们可以把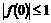 ,
,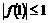 和
和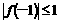 当成两个独立条件,先用
当成两个独立条件,先用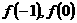 和
和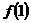 来表示
来表示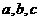 .
.
∵ 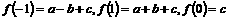 ,
,
∴ 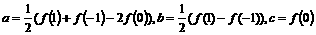 ,
,
∴ 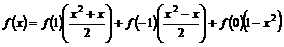 .
.
∴ 当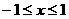 时,
时,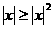 ,所以,根据绝对值不等式的性质可得:
,所以,根据绝对值不等式的性质可得:
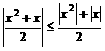 ,
,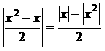 ,
,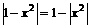
∴ 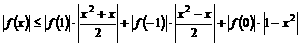
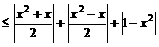
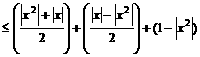
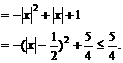
综上,问题获证.
5、已知函数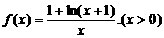
(1)函数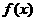 在区间(0,+
在区间(0,+ )上是增函数还是减函数?证明你的结论;
)上是增函数还是减函数?证明你的结论;
(2)若当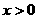 时,
时,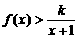 恒成立,求正整数
恒成立,求正整数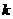 的最大值.
的最大值.
解:(1)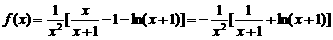
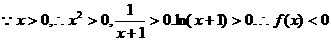 .
.
因此函数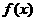 在区间(0,+∞)上是减函数.
在区间(0,+∞)上是减函数.
(2)(方法1)当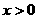 时,
时,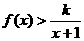 恒成立,令
恒成立,令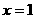 有
有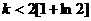
又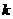 为正整数.
为正整数. 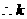 的最大值不大于3.……7′
的最大值不大于3.……7′
下面证明当
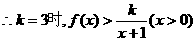 恒成立.
恒成立.
即证当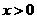 时,
时,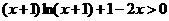 恒成立.
恒成立.
令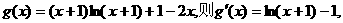
当
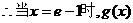 取得最小值
取得最小值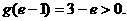
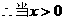 时,
时,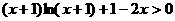 恒成立.
恒成立.
因此正整数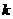 的最大值为3.
的最大值为3.
(2)(方法2)当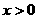 时,
时,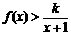 恒成立,
恒成立,
即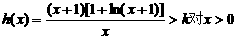 恒成立.
恒成立.
即 的最小值大于
的最小值大于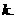
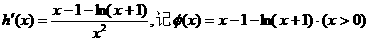
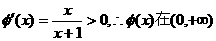 上连续递增,
上连续递增,
又
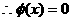 存在唯一实根
存在唯一实根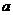 ,且满足:
,且满足: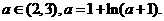
由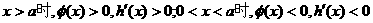 知:
知:
 的最小值为
的最小值为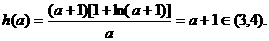
因此正整数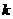 的最大值为3.
的最大值为3.
第2讲
4.x为何值时,不等式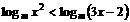 成立。
成立。
解:当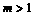 时,
时,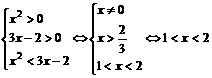
当 时,
时,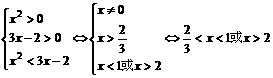
故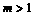 时,
时,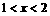
 时,
时,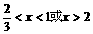 为所求。
为所求。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com