
题目列表(包括答案和解析)
5.(本小题满分12分)(2005年高考·全国卷Ⅰ·文19)
已知二次函数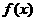 的二次项系数为a,且不等式
的二次项系数为a,且不等式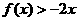 的解集为(1,3).
的解集为(1,3).
(1)若方程 有两个相等的根,求
有两个相等的根,求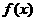 的解析式;
的解析式;
(2)若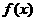 的最大值为正数,求a的取值范围.
的最大值为正数,求a的取值范围.
本小题主要考查二次函数、方程的根与系数关系,考查运用数学知识解决问题的能力.满分12分.
解:(Ⅰ)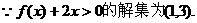
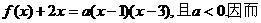
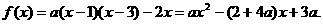 ①
①
由方程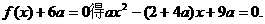 ②
②
因为方程②有两个相等的根,所以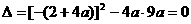 ,
,
即 
由于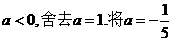 代入①得
代入①得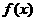 的解析式
的解析式
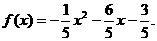
(Ⅱ)由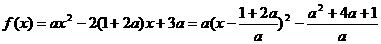
及
由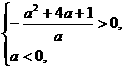 解得
解得 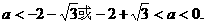
故当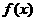 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是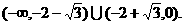
4.(2005年高考·浙江卷·理16文20)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
(Ⅲ)(文20)若h(x)=g(x)-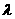 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数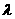 的取值范围.
的取值范围.
解:(Ⅰ)设函数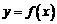 的图象上任意一点
的图象上任意一点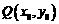 关于原点的对称点为
关于原点的对称点为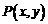 ,则
,则
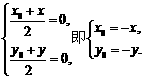
∵点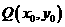 在函数
在函数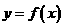 的图象上
的图象上
∴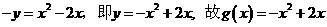
(Ⅱ)由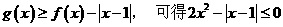
当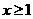 时,
时,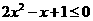 ,此时不等式无解
,此时不等式无解
当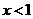 时,
时,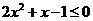 ,解得
,解得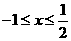

因此,原不等式的解集为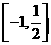

(Ⅲ)(文20)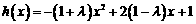
①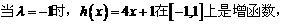
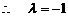
②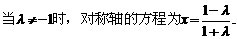
ⅰ)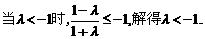
ⅱ)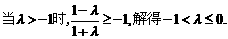
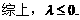
3.(本小题满分14分)(2005年高考·广东卷19)
设函数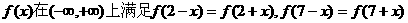 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有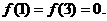 (Ⅰ)试判断函数
(Ⅰ)试判断函数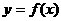 的奇偶性;
的奇偶性;
(Ⅱ)试求方程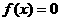 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
解: (I) 由于在闭区间[0,7]上,只有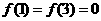 ,故
,故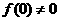 .若
.若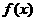 是奇函数,则
是奇函数,则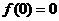 ,矛盾.所以,
,矛盾.所以,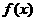 不是奇函数.
不是奇函数.
由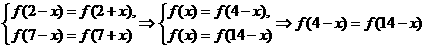
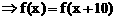 , 从而知函数
, 从而知函数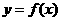 是以
是以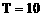 为周期的函数.
为周期的函数.
若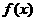 是偶函数,则
是偶函数,则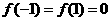 .又
.又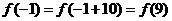 ,从而
,从而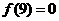 .
.
由于对任意的 (3,7]上,
(3,7]上,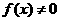 ,又函数
,又函数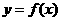 的图象的关于
的图象的关于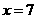 对称,所以对区间[7,11)上的任意
对称,所以对区间[7,11)上的任意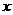 均有
均有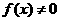 .所以,
.所以,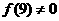 ,这与前面的结论矛盾.
,这与前面的结论矛盾.
所以,函数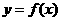 是非奇非偶函数.
是非奇非偶函数.
(II) 由第(I)小题的解答,我们知道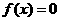 在区间(0,10)有且只有两个解,并且
在区间(0,10)有且只有两个解,并且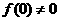 .由于函数
.由于函数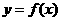 是以
是以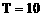 为周期的函数,故
为周期的函数,故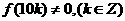 .所以在区间[-2000,2000]上,方程
.所以在区间[-2000,2000]上,方程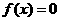 共有
共有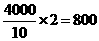 个解.
个解.
在区间[2000,2010]上,方程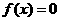 有且只有两个解.因为
有且只有两个解.因为
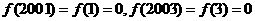 ,
,
所以,在区间[2000,2005]上,方程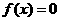 有且只有两个解.
有且只有两个解.
在区间[-2010,-2000]上,方程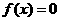 有且只有两个解.因为
有且只有两个解.因为
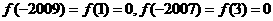 ,
,
所以,在区间[-2005,-2000]上,方程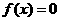 无解.
无解.
综上所述,方程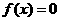 在[-2005,2005]上共有802个解.
在[-2005,2005]上共有802个解.
(2005年高考·浙江卷·理16)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|.
2.(本小题满分12分)(2005年春考·北京卷·文15)
记函数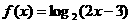 的定义域为集合M,函数
的定义域为集合M,函数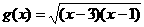 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
(2)集合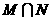 ,
, .
.
本小题主要考查集合的基本知识,考查逻辑思维能力和运算能力.满分12分.
解:(Ⅰ)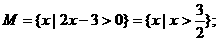
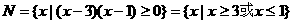
(Ⅱ)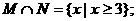
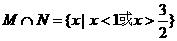 .
.
1.(本小题满分12分)(2005年春考·北京卷·理15)
设函数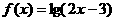 的定义域为集合M,函数
的定义域为集合M,函数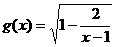 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
(2)集合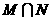 ,
, .
.
本小题主要考查集合的基本知识,考查逻辑思维能力和运算能力.满分12分.
解:(Ⅰ)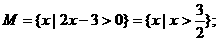
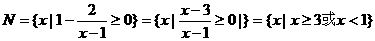
(Ⅱ)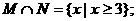
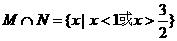 .
.
21.(2005年高考·全国卷Ⅰ·理13文13)若正整数m满足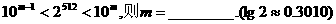 155
155
19.(2005年高考·天津卷·文15)设函数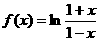 ,则函数
,则函数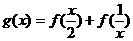 的定义域为__________
的定义域为__________ (2,1)È(1,2)
(2,1)È(1,2)
18.(2005年高考·天津卷·理16)设f(x)是定义在R上的奇函数,且y=f (x)的图象关于直线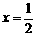 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________. 0
对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________. 0
17.(2005年高考·浙江卷·理11文11)函数y=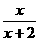 (x∈R,且x≠-2)的反函数是_________.
(x∈R,且x≠-2)的反函数是_________.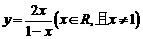
16.(2005年高考·江苏卷17)已知a,b为常数,若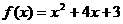 ,
,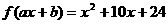 ,则
,则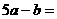 _________。2
_________。2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com